Cho tam giác DEF cân tại D, đường cao DH. Trên tia đối của tia HD lấy điểm M sao cho MH = DH.
a) Chứng minh DF = FM.
b) Trên tia đối của tia FE lấy điểm I sao cho FI = EF. Chứng minh rằng IE là tia phân giác của góc DIM.
c) Tia MF cắt DI tại N. Chứng minh MN là trung tuyến của tam giác DIM.
a) Chứng minh \(\Delta DHF = \Delta MHF\) (hai cạnh góc vuông) suy ra DF = FM (hai cạnh tương ứng).
b) Chứng minh \(\Delta DHI = \Delta MHI\) (hai cạnh góc vuông) suy ra \(\widehat {DIH} = \widehat {HIM}\) (hai góc tương ứng) suy ra IE là tia phân giác của góc DIM.
c) Chứng minh IH là đường trung tuyến của tam giác DIM và \(IF = \frac{2}{3}IH\) nên F là trọng tâm của tam giác DIM. Do đó MN là đường trung tuyến của tam giác DIM.
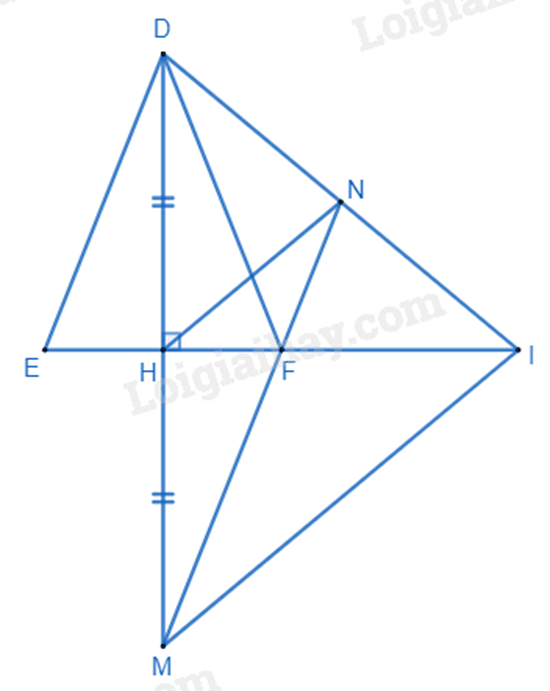
a) Xét \(\Delta DHF\) và \(\Delta MHF\) có:
DH = HM
\(\widehat {DHF} = \widehat {MHF}\left( { = {{90}^0}} \right)\)
HF chung
suy ra \(\Delta DHF = \Delta MHF\) (hai cạnh góc vuông)
suy ra DF = FM (hai cạnh tương ứng). (đpcm)
b) Xét \(\Delta DHI\) và \(\Delta MHI\) có:
\(DH = HM\)
\(\widehat {DHI} = \widehat {MHI}\left( { = {{90}^0}} \right)\)
HI chung
Suy ra \(\Delta DHI = \Delta MHI\) (hai cạnh góc vuông) suy ra \(\widehat {DIH} = \widehat {HIM}\) (hai góc tương ứng)
Mà IE nằm trong góc DIM suy ra IE là tia phân giác của góc DIM. (đpcm)
c) Vì \(\Delta DHI = \Delta MHI\) nên DI = IM (hai cạnh tương ứng) suy ra tam giác DIM cân tại I.
Mà IH \( \bot \) DH nên IH vừa là đường cao vừa là đường trung tuyến của tam giác DIM.
Do EH = HF (gt) và EF = FI (gt) nên \(\frac{{IF}}{{HI}} = \frac{{2HF}}{{3HF}} = \frac{2}{3}\) suy ra \(IF = \frac{2}{3}HI\) hay F là trọng tâm của tam giác DIM.
Chứng minh IH là đường trung tuyến của tam giác DIM và \(IF = \frac{2}{3}IH\) nên F là trọng tâm của tam giác DIM. Do đó MN là đường trung tuyến của tam giác DIM.
Mà MF cắt DI tại N nên MN là đường trung tuyên của tam giác DIM. (đpcm)
Các bài tập cùng chuyên đề
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:
Từ đẳng thức 2.12 = 8.3 ta có thể lập được bao nhiêu tỉ lệ thức?
Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2. Hãy biểu diễn y theo x?
Cho biết đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 12. Hệ số tỉ lệ là:
Biểu thức nào sau đây là đa thức một biến?
Giá trị của biểu thức \(7x - 4\) tại x = 9 là:
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Cho hình vẽ. So sánh độ dài các đoạn thẳng AB, AC, AD, AE.
Cho hình vẽ. Trong tam giác ABC, AD được gọi là
Tam giác ABC có hai đường cao AD và BE cắt nhau tại I. Khi đó, CI là
Cho tam giác ABC, tìm điểm O sao cho O cách đều ba đỉnh tam giác ABC
Tìm x, y biết:
a) \(\frac{x}{6} = \frac{4}{3}\)
b) \(7:x = - 9:4\)
c) \(\frac{x}{7} = \frac{y}{3}\) và \(x - y = - 16\)
Tổng kết cuối học kì 1, số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 3; 2. Biết tổng số học sinh giỏi của cả ba lớp là 45 em. Hỏi mỗi lớp 7A, 7B, 7C có bao nhiêu học sinh giỏi?
Ba thành phố ở ba địa điểm A, B, C không thẳng hàng như hình vẽ, biết AC = 30 km, AB = 90 km. Nếu đặt ở địa điểm C máy phát sóng truyền thanh có bán kính hoạt động 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
Cho ba số a, b, c khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\).
Tính giá trị của biểu thức \(M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\).
