Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

Ta biết rằng \(\sqrt 2 \) là một số vô tỉ và \(\sqrt 2  = 1,4142135624...\)

Gọi \(\left( {{r_n}} \right)\) là dãy số hữu tỉ dùng để xấp xỉ số \(\sqrt 2 ,\) với \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,4142;...\)

a) Dùng máy tính cầm tay, hãy tính: \({3^{{r_1}}};{3^{{r_2}}};{3^{{r_3}}};{3^{{r_4}}}\) và \({3^{\sqrt 2 }}.\)

b) Có nhận xét gì về sai số tuyệt đối giữa \({3^{\sqrt 2 }}\) và \({3^{{r_n}}},\) tức là \(\left| {{3^{\sqrt 2 }} - {3^{{r_n}}}} \right|,\) khi n càng lớn?

Sử dụng máy tính cầm tay, tính các luỹ thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):

a) \(1,{2^{1,5}}\);                  

b) \({10^{\sqrt 3 }}\);              

c) \({\left( {0,5} \right)^{ - \frac{2}{3}}}\).

Ta biết rằng, \(\sqrt 2 \) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2  = 1,414213562...\)

Cũng có thể coi \(\sqrt 2 \) là giới hạn của dãy số hữu tỉ \(\left( {{r_n}} \right)\):

\(1,4;1,41;1,414;1,4142;...\)

Từ đây, ta lập dãy số các luỹ thừa \(\left( {{3^{{r_n}}}} \right)\).

a) Bảng dưới cho biết những số hạng đầu tiên của dãy số \(\left( {{3^{{r_n}}}} \right)\) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.

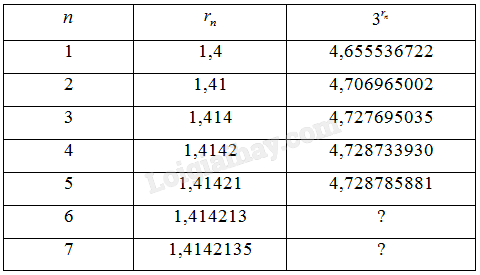
b) Nêu nhận xét về dãy số \(\left( {{3^{{r_n}}}} \right)\).

Rút gọn biểu thức: \({\left( {{x^{\sqrt 2 }}y} \right)^{\sqrt 2 }}\left( {9{y^{ - \sqrt 2 }}} \right)\) (với \(x,y > 0\)).

Viết các biểu thức sau dưới dạng một luỹ thừa \(\left( {a > 0} \right)\):

a) \({a^{\frac{3}{5}}}.{a^{\frac{1}{2}}}:{a^{ - \frac{2}{5}}}\);    

b) \(\sqrt {{a^{\frac{1}{2}}}\sqrt {{a^{\frac{1}{2}}}\sqrt a } } \).

a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ số thập phân thứ năm).

b) Từ kết quả quả ở câu a, có dự đoán gì về tính chất của phép tính luỹ thừa với số mũ thực?

Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm):

a) \( (-2,7)^{-4}\).

b) \( \sqrt 3 - 1)^{\sqrt[3] {4} + 1}\).

Không sử dụng máy tính cầm tay, hãy so sánh các số: \({2^{2\sqrt 3 }}\,\,và \,\,{2^{3\sqrt 2 }}\).

So sánh \({10^{\sqrt 2 }}\,\,và \,\,10\).

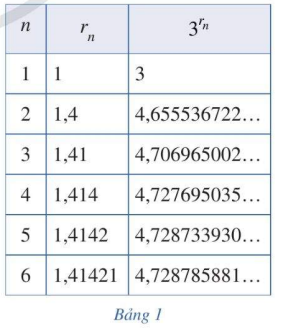
Xét số vô tỉ: \(\sqrt 2  = 1,4142135624...\). Xét dãy số hữu tỉ: \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) và \(\lim {r_n} = \sqrt 2 \). Bằng cách tính \({3^{{r_n}}}\) tương ứng, ta nhận được Bảng 1 ghi các dãy số \(\left( {{r_n}} \right)\) và \(\left( {{3^{{r_n}}}} \right)\) với n = 1, 2, …, 6. Người ta chứng minh được rằng khi \(n \to  + \infty \) thì dãy số \(\left( {{3^{{r_n}}}} \right)\) dần đến một giới hạn mà ta gọi là \({3^{\sqrt 2 }}\). Nêu dự đoán về giá trị của số \({3^{\sqrt 2 }}\) (đến hàng phần trăm).

Tính:

a) \(\sqrt[3]{{ - 27}}\)

b)\({25^{\frac{3}{2}}}\);

c) \({32^{ - \frac{2}{5}}}\)

d)\({\left( {\frac{{27}}{8}} \right)^{\frac{2}{3}}}\).

Điều kiện xác định của \({x^{\sqrt 2 }}\) là:

A. \(x \in \mathbb{R}\)

B. \(x \ne 0\)

C. \(x \ge 0\)

D. \(x > 0\)

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).