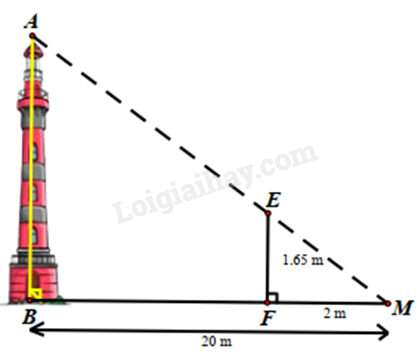
Trong hình bên, biết MB = 20m, MF = 2m, EF = 1,65m. Tính chiều cao AB của ngọn hải đăng.
-
A.
16,5 m.
-
B.
165 m.
-
C.
16,5 cm.
-
D.
0,65 m.
Dựa vào hệ quả của định lí Thales để tính AB.
Vì EF // AB nên \(\frac{{AB}}{{EF}} = \frac{{BM}}{{MF}}\)\( \Rightarrow AB = \frac{{BM.EF}}{{MF}} = \frac{{20.1,65}}{2} = 16,5\left( m \right)\)
Đáp án : A
Các bài tập cùng chuyên đề
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = 6 - 2x\)?
Đường thẳng song song với đường thẳng y = 3x và cắt trục tung tại điểm có tung độ bằng 2 là:
Cho hai đường thẳng \(y = - \frac{1}{3}x + 2\) và \(y = \frac{1}{3}x + 2\). Hai đường thẳng đã cho:
Cho AB = 16cm. CD = 3dm. Tỉ số \(\frac{{AB}}{{CD}}\) là:
Cho tam giác ABC, \(D \in AB,E \in AC\) (như hình vẽ). Khẳng định nào sau đây là đúng?
Cho hai hàm số bậc nhất : \({d_1}\): y = 2x - 3 và \({d_2}\): y = x – 2 .
a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của hai đồ thị hàm số trên.
c) Xác định a, b của hàm số bậc nhất y = ax + b, (a \( \ne \) 0) biết rằng đồ thị hàm số \({d_3}\) của hàm số y = ax + b song song với \({d_1}\) và cắt đường thẳng \({d_2}\) tại B có hoành độ bằng -1.
Rừng ngập mặn Cần Giờ (còn gọi là rừng Sác), trong chiến tranh bom đạn và chất độc hóa học đã làm nơi đây trở thành "vùng đất chết"; được trồng lại từ năm 1979, nay đã trở thành "lá phổi xanh" cho Thành phố Hồ Chí Minh, được UNESCO công nhận là khu dự trữ sinh quyên của thế giới đầu tiên ở Việt Nam vào ngày 21/01/2000. Diện tích rừng phủ xanh được cho bởi hàm số \(S = 3,14 + 0,05t\), trong đó S tính bằng nghìn hécta, t tính bằng số năm kể từ năm 2000.
a) Tính diện tích rừng Sác được phủ xanh vào năm 2023.
b) Diện tích rừng Sác được phủ xanh đạt 4,04 nghìn hécta vào năm nào?
Bạn An đo được khoảng cách từ vị trí mình đứng (điểm K) đến cây D và cây E ở hai bên hồ nước lần lượt là KD = 18m và KE = 20,25m. Để tính độ dài DE, An xác định điểm A nằm giữa K, D và điểm E nằm giữa K, E sao cho KA = 6,4m, KB = 7,2m và khoảng cách giữa A và B là 32m.
a) Chứng minh \(\frac{{KB}}{{KE}} = \frac{{AK}}{{AD}}\).
b) Chứng minh \(AB//DE\).
c) Tính khoảng cách giữa D và E.
Cho tam giác ABC có BC = 20cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K kẻ các đường EF và MN song song với BC (E, M \( \in \) AB, F, N \( \in \) AC).
a) Tính độ dài các đoạn MN và EF.
b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là \(300c{m^2}\).
Cho đường thẳng d: y = (2m + 1)x – 1. Tìm m để d cắt 2 trục tọa độ tạo thành tam giác có diện tích bằng \(\frac{1}{2}\).
