Đề bài
Cho hình chóp S. ABCD với ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Đường thẳng OE nằm trong mặt phẳng nào?
-
A.
(SAC).
-
B.
(SBD).
-
C.
(SDC).
-
D.
(SAB).
Phương pháp giải
Sử dụng kiến thức đường thẳng nằm trong mặt phẳng: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải của GV Loigiaihay.com
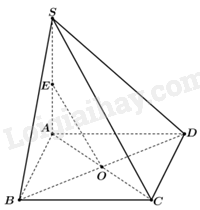
Do \(O \in AC \subset \left( {SAC} \right),E \in SA \subset \left( {SAC} \right)\) nên đường thẳng OE nằm trong mặt phẳng (SAC)
Đáp án : A








Danh sách bình luận