Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. M là điểm nằm trên cạnh BC sao cho \(MB = 2MC\). Chứng minh rằng MG // (ACD).
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
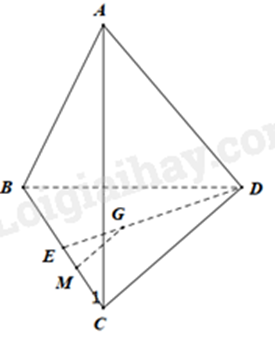
Gọi E là trung điểm của BC. Vì G là trọng tâm của tam giác BCD nên \(\frac{{GD}}{{ED}} = \frac{2}{3}\)
Mà \(MB = 2MC \Rightarrow 3MC = BC\). Lại có: \(EC = BE = \frac{1}{2}BC \Rightarrow \frac{{MC}}{{EC}} = \frac{2}{3}\)
Tam giác EDC có: \(\frac{{GD}}{{ED}} = \frac{{MC}}{{EC}}\left( { = \frac{2}{3}} \right)\) nên MG // CD (định lý Thalès đảo)
Mà \(CD \subset \left( {ACD} \right)\) nên MG // (ACD)
Các bài tập cùng chuyên đề
Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là:
Chọn đáp án đúng
Nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là:
Tập xác định của D của hàm số \(y = \cot x\) là:
Hàm số \(y = \tan x\)tuần hoàn với chu kì là:
Độ dài của 60 lá dương xỉ trưởng thành được cho bằng mẫu số liệu ghép nhóm sau:
Tần số của nhóm [30;40) là:
Trong các dãy số sau, dãy số nào là dãy số tăng?
Trong các dãy số sau, dãy số nào là cấp số cộng?
Dãy số nào dưới đây được viết dưới dạng công thức của số hạng tổng quát?
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\). Chọn đáp án đúng
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n}\) bằng:
Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right)\) là:
Cho lăng trụ tam giác ABC.A’B’C’. Khẳng định nào sau đây là đúng?
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Kết luận nào sau đây là đúng?
Cho hai đường thẳng a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
Hình chóp tứ giác có mặt bên là hình gì?
Nếu d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì:
Cho tứ diện ABCD. Chọn đáp án đúng.
Khảo sát thời gian tập thể dục trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là:
