Một sóng cơ truyền dọc theo một sợi dây đàn hồi rất dài với biên độ 8 mm. Tại một thời điểm, hai phần tử trên dây cùng lệch khỏi vị trí cân bằng 4 mm, chuyển động ngược chiều và cách nhau một khoảng ngắn nhất là 7 cm (tính theo phương truyền sóng). Gọi s là ti số của tốc độ dao động cực đại của một phần tử trên dây với tốc độ truyền sóng, δ gần giá trị nào nhất sau đây?

Hai phần tử gần nhau nhất có độ lớn li độ \(\frac{A}{2}\) chuyển động ngược chiều nhau vậy hai điểm đó đối xứng với nhau qua hai bên

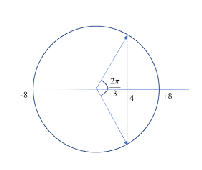
\(\frac{{2\pi d}}{\lambda } = \frac{{2\pi }}{3} \Rightarrow d = \frac{\lambda }{3} = 7cm \Rightarrow \lambda  = 21cm\)

Tốc độ truyền sóng trên dây và tốc độ dao động cực đại của phần tử trên dây lần lượt là

\(\left\{ \begin{array}{l}v = \frac{\lambda }{T}\\{v_{\max }} = \lambda A = \frac{{2\pi }}{T}A\end{array} \right. \Rightarrow \delta  = \frac{{{v_{\max }}}}{v} = \frac{{2\pi A}}{\lambda } = \frac{{2\pi {{.8.10}^{ - 3}}}}{{0,21}} = 0,239\)