Cho tam giác ABC như hình bên dưới.
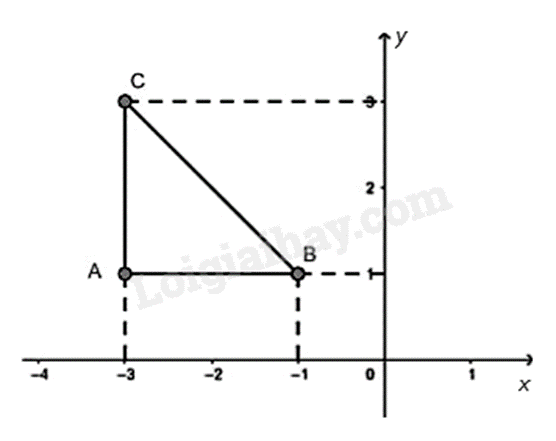
a) Xác định tọa độ các điểm A, B, C.
b) Tam giác ABC có là tam giác vuông cân hay không ?
c) Xác định tọa độ điểm D để tứ giác ABDC là hình vuông.
a) Quan sát đồ thị để xác định tọa độ của các điểm.
b) Chứng minh AB \( \bot \) AC và AB = AC.
c) Để ABDC là hình vuông thì \(\widehat {ACD} = \widehat {ABD} = {90^0}\) và \(AB = BC = CD = DA\).
a) Hình chiếu của điểm A trên trục hoành là -3 và trên trục tung là 1. Do đó tọa độ của điểm A là \(A\left( { - 3;1} \right)\).
Hình chiếu của điểm B trên trục hoành là -1 và trên trục tung là 1. Do đó tọa độ của điểm A là \(B\left( { - 1;1} \right)\).
Hình chiếu của điểm C trên trục hoành là -3 và trên trục tung là 3. Do đó tọa độ của điểm A là \(C\left( { - 3;3} \right)\).
Vậy tọa độ của các điểm là: \(A\left( { - 3;1} \right)\); \(B\left( { - 1;1} \right)\); \(C\left( { - 3;3} \right)\).
b) Quan sát hình vẽ, ta thấy
\(\left. \begin{array}{l}AB//Ox\\AC//Oy\\Ox \bot Oy\end{array} \right\} \Rightarrow AB \bot AC \Rightarrow \widehat A = {90^0}\)
Mà AB = AC (= 2)
\( \Rightarrow \Delta ABC\) vuông cân tại A.
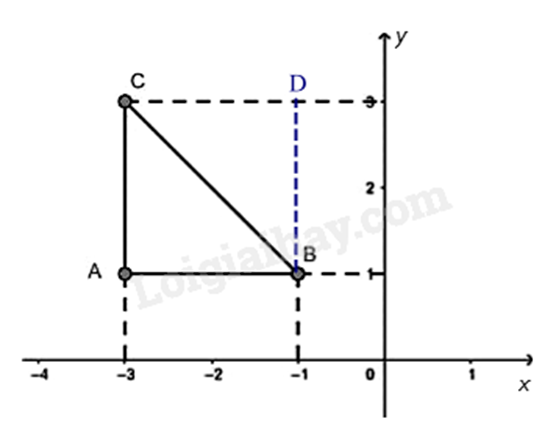
c) Ta có: \(\Delta ABC\) vuông cân tại A nên để ABDC là hình vuông thì \(\widehat {ACD} = \widehat {ABD} = {90^0}\) và AB = BC = CD = DA hay \(AC \bot CD;AB \bot BD\).
Qua điểm C kẻ đường thẳng vuông góc với Oy.
Qua điểm B kẻ đường thẳng vuông góc với Ox.
Hai đường thẳng này cắt nhau tại điểm D.
CD cắt trục tung tại điểm có tung độ bằng 3.
BD cắt trục hoành tại điểm có hoành độ bằng -1.
=> Tọa độ điểm D là \(D\left( { - 1;3} \right)\).
Vậy để ABDC là hình vuông thì \(D\left( { - 1;3} \right)\).








Danh sách bình luận