Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB = 8cm, O là trung điểm của AC. Độ dài đoạn SO là:
-
A.
\(8\sqrt 2 \)cm.
-
B.
6cm.
-
C.
\(\sqrt {32} \)cm.
-
D.
4cm.
Sử dụng công thức tính thể tích hình chóp tứ giác đều.
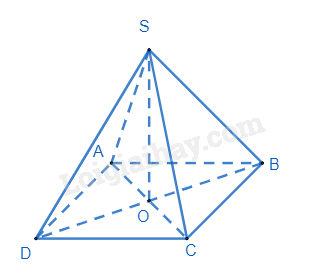
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, O là trung điểm của AC nên SO là đường cao của hình chóp S.ABCD.
Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} = {8^2} + {8^2} = 128\\ \Rightarrow AC = \sqrt {128} = 8\sqrt 2 \\ \Rightarrow AO = \frac{{8\sqrt 2 }}{2} = 4\sqrt 2 \end{array}\)
Vì tam giác SAB đều nên SA = AB = 8cm. Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có:
\(\begin{array}{l}S{O^2} = S{A^2} - A{O^2} = {8^2} - {\left( {4\sqrt 2 } \right)^2} = 32\\ \Rightarrow SO = \sqrt {32} \end{array}\)
Đáp án : C
