Cho đoạn thẳng \(ABC\) , điểm \(I\) nằm trong tam giác. Các tia \(AI,\,BI,CI\) cắt các cạnh \(BC,\,AC,\,AB\) theo thứ tự ở \(D,\,E,\,F\) . Tổng \(\frac{{AF}}{{FB}} + \frac{{AE}}{{EC}}\) bằng tỉ số nào dưới đây?
-
A.
\(\frac{{AI}}{{AD}}\)
-
B.
\(\frac{{AI}}{{ID}}\)
-
C.
\(\frac{{BD}}{{DC}}\)
-
D.
\(\frac{{DC}}{{DB}}\)
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
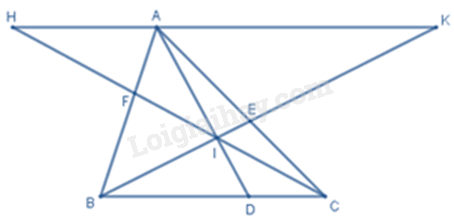
Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt \(CF,\,BE\) lần lượt tại \(H,K\) .
\(AH // BC\) nên theo hệ quả định lí Thalès ta có \(\frac{{AF}}{{BF}} = \frac{{AH}}{{BC}}\)
\(AK // BC\) nên theo hệ quả định lí Thalès ta có \(\frac{{AE}}{{EC}} = \frac{{AK}}{{BC}}\)
\( \Rightarrow \frac{{AF}}{{BF}} + \frac{{AE}}{{EC}} = \frac{{AH}}{{BC}} + \frac{{AK}}{{BC}} = \frac{{HK}}{{BC}}\) (1)
Lại có \(AH // DC\) nên theo định lí Thalès ta có \(\frac{{AI}}{{ID}} = \frac{{AH}}{{CD}}\)
\(AK // BD\) nên theo định lí Thalès ta có \(\frac{{AI}}{{ID}} = \frac{{AK}}{{BD}}\)
Do đó \(\frac{{AI}}{{ID}} = \frac{{AH}}{{CD}} = \frac{{AK}}{{BD}}\) (2)
Theo tính chất dãy tỉ số bằng nhau \(\frac{{AH}}{{CD}} = \frac{{AK}}{{BD}} = \frac{{AH + AK}}{{CD + BD}} = \frac{{HK}}{{BC}}\) (3)
Từ (2) và (3) \( \Rightarrow \frac{{AI}}{{ID}} = \frac{{HK}}{{BC}}\) (4)
Từ (1) và (4) \( \Rightarrow \frac{{AF}}{{BF}} + \frac{{AE}}{{EC}} = \frac{{AI}}{{ID}}\)
Đáp án : B
