Cho tam giác \(ABC\) có \(AB = 12{\rm{ cm}}\) , điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 8{\rm{ cm}}\) . Kẻ \(DE\) song song với \(BC\,\left( {E \in AC} \right)\) , kẻ \(EF\) song song với \(CD\,\left( {F \in AB} \right)\) . Tính độ dài \(AF\) .
-
A.
2 cm
-
B.
\(\frac{4}{3}\) cm
-
C.
3 cm
-
D.
\(\frac{{16}}{3}\) cm
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
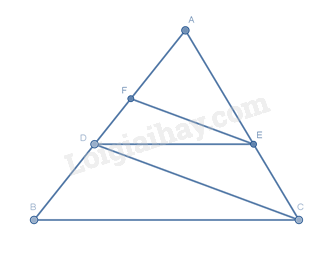
Xét tam giác \(ABC\) có \(DE // BC\) nên theo định lí Thalès ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ACD\) có \(EF // CD\) nên theo định lí Thalès ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (2)
Từ (1), (2) suy ra \(\frac{{AD}}{{AB}} = \frac{{AF}}{{AD}} \)
\(AF.AB = A{D^2}\)
\(AF = \frac{{A{D^2}}}{{AB}} = \frac{{{8^2}}}{{12}} = \frac{{16}}{3}\)
Đáp án : D
