Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây. Biết phương trình dao động tại đầu A là \({u_A} = a\cos 1{\rm{00}}\pi t\). Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b \(\left( {b \ne {\rm{0}}} \right)\)cách đều nhau và cách nhau khoảng 1 m. Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:
-
A.
\(a\sqrt 2 ;v = 2{\rm{00}}m/s\)
-
B.
\(a\sqrt 3 ;v = 15{\rm{0}}m/s\)
-
C.
\(a;v = 3{\rm{00}}m/s\)
-
D.
\(a\sqrt 2 ;v = 1{\rm{00}}m/s\)
Đáp án : A
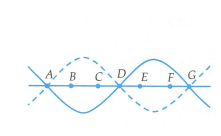
Các điểm B, C, E, F dao động cùng biên độ b sẽ cách nút gần nó nhất những khoảng bằng nhau:
AB = CD = DE = FG
Mặt khác, các điểm B, C, E, F cách đều nhau khoảng lm nên ta có
BC = CE = EF = 1m
Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}CE = CD + DE\\CD = DE\end{array} \right. \Rightarrow CE = 2CD \Rightarrow BC = 2CD \Rightarrow BC = AB + CD\)
Mặt khác \(AB + BC + CD = \frac{\lambda }{2} \Rightarrow 2BC = \frac{\lambda }{2} \Rightarrow \lambda = 2.2.1 = 4m \Rightarrow \lambda f = 4.5{\rm{0}} = 2{\rm{00}}\)
Biên độ là \(b = 2a\left| {\sin \frac{{2\pi AB}}{\lambda }} \right| = 2a\left| {\sin \frac{{2\pi \frac{{AD}}{4}}}{\lambda }} \right| = 2a\left| {\sin \frac{{2\pi \frac{\lambda }{8}}}{\lambda }} \right| = a\sqrt 2 \)
Đáp án A.
Các bài tập cùng chuyên đề
Trên một sợi dây đàn hồi dài 1m, hai đầu cố định, đang có sóng dừng với 5 nút sóng (kể cả hai đầu dây). Bước sóng của sóng truyền trên dây là:
Một sợi dây đàn hồi đang có sóng dừng. Trên dây, những điểm dao động với cùng biên độ A1 có vị trí cân bằng liên tiếp cách đều nhau một đoạn d1 và những điểm dao động với cùng biên độ A2 có vị trí cân bằng liên tiếp cách đều nhau một đoạn d2. Biết A1 > A2 > 0. Biểu thức nào sau đây đúng?
M, N, P là 3 điểm liên tiếp nhau trên một sợi dây mang sóng dừng có cùng biên độ 4 mm, dao động tại N ngược pha với dao động tại M \(MN = \frac{{NP}}{2} = 1\)cm. Cứ sau khoảng thời gian ngắn nhất là 0,04 s sợi dây có dạng một đoạn thắng. Tốc độ dao động của phần tử vật chất tại điểm bụng khi qua vị trí cân bằng (lấy \(\pi = 3,14\))
Cho sợi dây có chiều dài l, hai đầu dây cố định, vận tốc truyền sóng trên sợi dây không đổi. Khi tần số sóng là f1 = 50Hz trên sợi dây xuất hiện n1 = 16 nút sóng. Khi tần số sóng là f2, trên sợi dây xuất hiện n2 = 10 nút sóng. Tính tần số f2.
Quan sát hiện tượng sóng dừng trên một sợi dây có chiều dài 36 cm, người ta thấy trên sợi dây hình thành ra 5 nút sóng, trong đó có 2 nút nằm tại hai đầu sợi dây. Khoảng thời gian giữa hai lần gần nhất mà sợi dây duỗi thẳng là 0,6 s. Vận tốc truyền sóng trên sợi dây là:
Làm thí nghiệm giao thoa về sóng dừng trên sợi dây có chiều dài l, hai đầu cố định, tần số thay đổi được. Khi tần số là f1 = 45Hz thì trên dây có hiện tượng sóng dừng. Khi tăng tần số của nguồn sóng, tới khi tần số là f2 = 54Hz thì trên sợi dây mới lại xuất hiện sóng dừng. Hỏi tần số của nguồn nhỏ nhất bằng bao nhiêu thì trên sợi dây bắt đầu có sóng dừng? Cho biết vận tốc truyền sóng trên sợi dây không đổi
Một sợi dây AB có chiều dài l, đầu A cố định, đầu B gắn với cần rung với tần số thay đổi được, điểm B được coi là nút sóng. Ban đầu trên dây có sóng dừng, khi tần số tăng thêm 40 Hz thì số nút trên dây tăng thêm 8 nút. Tính thời gian để sóng truyền đi giữa hai đầu dây?
Xét sóng dừng trên một sợi dây với một đầu dây buộc vào điểm cố định, đầu còn lại gắn với cần rung có tần số f = 20Hz. Tốc độ truyền sóng trên dây là v = 120cm/s. Tìm số nút và bụng sóng trên một đoạn dây nằm sát đầu cố định và có chiều dài l = 22,1cm.
Sóng dừng trên sợi dây có chiều dài l, bước sóng \(\lambda = 16cm\). Xét điểm O trùng với một nút sóng, các điểm M, N, P, Q nằm về một phía của điểm O cách O những đoạn tương ứng là: 59 cm; 87 cm; 106 cm; 143 cm. Pha dao động của các điểm trên có tính chất gì?
Một sợi dây đàn hồi có sóng dừng, biên độ tại bụng sóng là A0, vận tốc truyền sóng trên dây
v = 240 cm/s. Điểm M trên dây có phương trình dao động \({u_M} = \frac{{{A_{\rm{0}}}}}{{\sqrt 2 }}\cos \left( {2{\rm{0}}\pi t + \frac{\pi }{4}} \right)cm\)thì điểm N cách M một đoạn 11 cm dao động với phương trình:
Cho sợi dây một đầu cố định, một đầu còn lại gắn với cần rung phát sóng dao động với phương trình \({u_{\rm{0}}} = a\cos \left( {\omega t + \varphi } \right)\) cm. Trên dây có sóng dừng ổn định với bước sóng. Hai điểm M và N trên dây cách nhau \(3,75\lambda \) có biên độ lần lượt là AM= 6cm; AN= 8cm. Tìm biên độ của nguồn phát ra sóng đó?
Ba điểm A, B, C là ba điểm liên tiếp trên một sợi dây có sóng dừng với cùng biên độ \(4\sqrt 3 \) cm. Điểm A dao động ngược pha với điểm B và AB = 2BC. Cứ sau những khoảng thời gian liên tiếp là
0,25 s thì sợi dây có dạng một đoạn thẳng. Tìm tốc độ dao động cực đại của điểm M là trung điểm của AC?
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây A là một điểm nút, B là một điểm bụng gần A nhất, AB = 14 cm, gọi C là một điểm trong khoảng AB có biên độ bằng một nửa biên độ của B. Khoảng cách AC là:
Một sợi dây AB đàn hồi căng ngang dài l = 120cm, hai đầu cố định đang có sóng dừng ổn định. Bề rộng của bụng sóng là 4a . Khoảng cách gần nhất giữa hai điểm dao động cùng pha có cùng biên độ bằng a là 20 cm. Số bụng sóng trên AB là
Một sợi dây sắt, mảnh, dài 120 cm căng ngang, có hai đầu cố định. Ớ phía trên, gần sợi dây có một nam châm điện được nuôi bằng nguồn điện xoay chiều có tần số 50 Hz. Trên dây xuất hiện sóng dừng với 2 bụng sóng. Tốc độ truyền sóng trên dây là
Một sợi dây đàn hồi dài 30 cm có hai đầu cố định. Trên dây đang có sóng dừng. Biết sóng truyền trên dây với bước sóng 20 cm và biên độ dao động của điểm bụng là 2 cm. Số điểm trên dây mà phần tử tại đó dao động với biên độ 6 mm là
