Đề bài
Cho ba mặt phẳng \(\left( \alpha \right),\left( \beta \right),\left( \gamma \right)\) đôi một song song. Hai đường thẳng \(d,d'\) lần lượt cắt ba mặt phẳng này \(A,B,C\) và \(A',B',C'\) (\(B\) nằm giữa \(A\) và \(C\), \(B'\) nằm giữa \(A'\) và \(C'\)). Giả sử \(AB = 5,BC = 4,A'C' = 18\). Tính độ dài hai đoạn thẳng \(A'B',B'C'\).
-
A.
\(A'B' = 10,B'C' = 8\).
-
B.
\(A'B' = 8,B'C' = 10\).
-
C.
\(A'B' = 12,B'C' = 6\).
-
D.
\(A'B' = 6,B'C' = 12\).
Phương pháp giải
Sử dụng định lí Thalès trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.
Lời giải của GV Loigiaihay.com
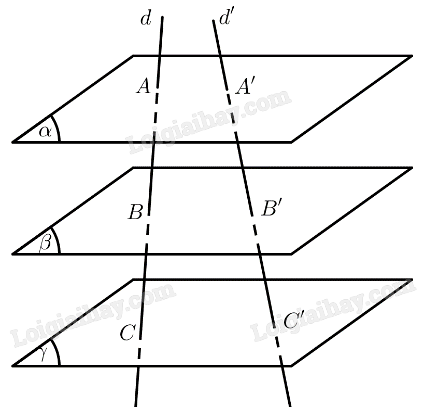
Ta có: \(AC = AB + BC = 5 + 4 = 9\)
Theo định lí Thalès trong không gian ta có:
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} \Leftrightarrow A'B' = \frac{{AB.A'C'}}{{AC}} = \frac{{5.18}}{9} = 10\\ \Rightarrow B'C' = A'C' - A'B' = 18 - 10 = 8\end{array}\)
Đáp án : A
