Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\), \(N\) lần lượt là trung điểm của \(AD\) và \(BC\). Giao tuyến của \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là
-
A.
\(SK\) (\(K\) là trung điểm của \(AB\)).
-
B.
\(SO\) (\(O\) là tâm của hình bình hành \(ABCD\)).
-
C.
\(SF\) (\(F\) là trung điểm của \(CD\)).
-
D.
\(SD\).
Phương pháp giải
Để tìm giao tuyến của hai mặt phẳng (P), (Q) ta tìm điểm chung thuộc cả 2 mặt (P), (Q).
Tức là, \(\left. \begin{array}{l}A \in (P) \cap (Q)\\B \in (P) \cap (Q)\end{array} \right\} \Rightarrow (P) \cap (Q) = AB\)
Lời giải của GV Loigiaihay.com
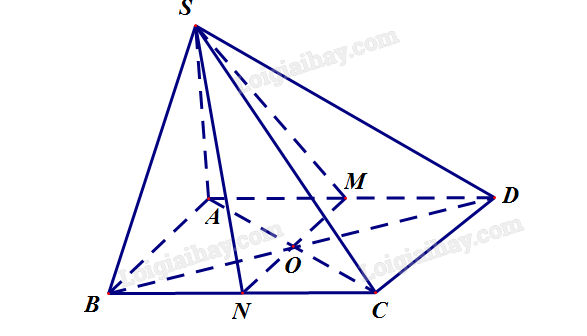
Gọi \(O\) là tâm hình bình hành \(ABCD\) \( \Rightarrow O = AC \cap MN\)
Dễ thấy,\(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) có chung điểm S,O\( \Rightarrow SO = \left( {SMN} \right) \cap \left( {SAC} \right)\).
Vậy SO là giao tuyến của \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\)
Đáp án : B
