Đề bài
Xác định các khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\).
-
A.
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right)\).
-
B.
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
-
C.
\(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
-
D.
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Phương pháp giải
Quan sát đồ thị hàm số \(y = \tan x\).
Lời giải của GV Loigiaihay.com
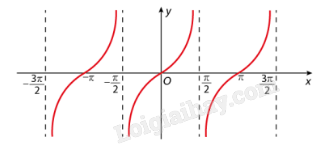
Khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\) là \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Đáp án : D
