Cho tam giác ABC có AB = AC. Trên cạnh BC lấy điểm D sao cho \(B{\rm{D}} = \frac{1}{2}DC\) . Kẻ BH, CK vuông góc với AD, \(H \in A{\rm{D}},K \in A{\rm{D}}\) . Khẳng định nào dưới đây là đúng:

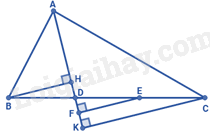
Gọi E là trung điểm của CD

Suy ra BD = DE = EC

Từ E kẻ \({\rm{EF}} \bot A{\rm{D}};F \in A{\rm{D}}\)

Ta có: \({\rm{EF}} \bot A{\rm{D}};CK \bot A{\rm{D}};//CK \Rightarrow F\) là trung điểm của DK.

Suy ra EF là đường trung bình của tam giác DKC.

\( \Rightarrow {\rm{EF = }}\frac{1}{2}CK\)

Xét tam giác vuông BHD và tam giác vuông EFD có:

\(\widehat {B{\rm{D}}H} = \widehat {E{\rm{D}}F}\) (đối đỉnh)

BD = ED ( chứng minh trên)

Do đó: \(\Delta BH{\rm{D}} = \Delta {\rm{EFD}}\) (cạnh huyền – góc nhọn)

Suy ra: BH = EF

Vậy \(BH = \frac{1}{2}CK\) hay CK = 2BH là khẳng định đúng.