Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây.
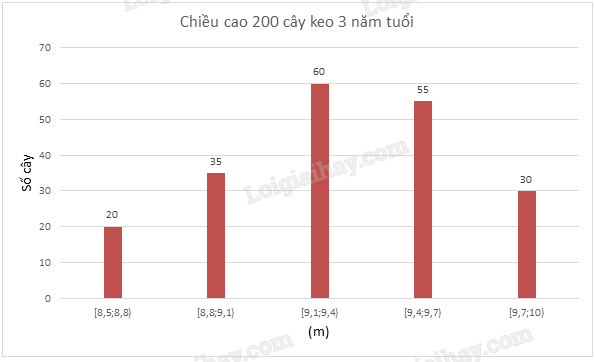
Số trung bình và mốt của mẫu số liệu ghép nhóm trên lần lượt là
-
A.
\(9,31;9,45\).
-
B.
\(9,41;9,35\).
-
C.
\(9,31;9,35\).
-
D.
\(9,31;9,65\)
* Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline X \)
\(\overline X = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)
Trong đó, \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\)
(với \(i = 1,...,k)\) là giá trị đại diện của nhóm \(\left[ {{a_i};\;{a_{i + 1}}} \right)\)
* Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_o}\), được xác định bởi công thức \({M_o} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}} \cdot \left( {{u_{m + 1}} - {u_m}} \right)\)
Chiều cao của 200 cây keo được thống kê như bảng sau:
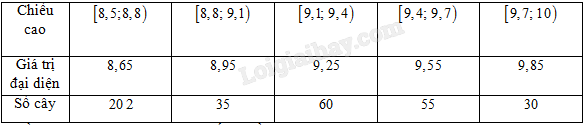
Chiều cao trung bình của 200 cây xấp xỉ bằng:
\(\left( {8,65.20 + 8,95.35 + 9,25.60 + 9,55.55 + 9,85.30} \right):200 = 9,31\left( {{\rm{\;m}}} \right)\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {9,1;9,4} \right)\)
Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)
Mốt của mẫu số liệu trên là:
\({M_0} = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}} \cdot 0,3 = 9,35\left( {{\rm{\;m}}} \right)\)
Đáp án : C








Danh sách bình luận