Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB\)//\(CD\) và \(AB = 2CD\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Lấy \(E\) thuộc cạnh \(SA\), \(F\) thuộc cạnh \(SC\) sao cho \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SC}} = \frac{2}{3}\) .
Thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( {BEF} \right)\) là
-
A.
Một tam giác.
-
B.
Một tứ giác.
-
C.
Một hình thang.
-
D.
Một hình bình hành.
Muốn tìm thiết diện của một hình chóp với mặt phẳng \(\left( \alpha \right)\) cho trước, ta cần tìm các “đoạn giao tuyến” của \(\left( \alpha \right)\) với các mặt của hình chóp. Thiết diện cần tìm chính là đa giác giới hạn với các đoạn giao tuyến vừa tìm được.
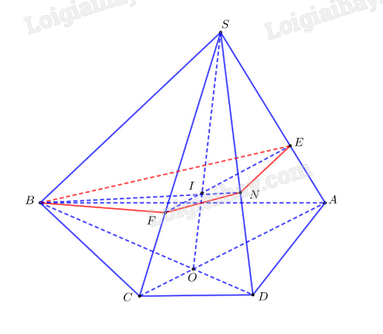
Ta có: \(\left\{ \begin{array}{l}(BEF) \cap (SBC) = BF\\(BEF) \cap (SAB) = BE\end{array} \right.\)
Trong \(\left( {SBD} \right)\), gọi \(N = BI \cap SD\) \( \Rightarrow \)\(N \in (BEF) \cap (SAD)\)
Mà \(E \in (BEF) \cap (SAD)\)
\( \Rightarrow \)\((BEF) \cap (SAD) = NE\)
\( \Rightarrow \) \((BEF) \cap (SCD) = NF\)
Vậy thiết diện của hình chóp cắt bởi mặt phẳng \(\left( {BEF} \right)\) là tứ giác \(BFNE\).
Đáp án : B







