Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. \(M,\,N\) lần lượt thuộc đoạn \(AB,\,SC\,.\) Khẳng định nào sau đây đúng?
-
A.
Giao điểm của \(MN\) và \(\left( {SBD} \right)\) là giao điểm của \(MN\) và \(SD\)
-
B.
Đường thẳng \(MN\) không cắt mặt phẳng \(\left( {SBD} \right)\).
-
C.
Giao điểm của \(MN\) và \(\left( {SBD} \right)\) là giao điểm của \(MN\) và \(SI\), trong đó \(I\) là giao điểm của \(CM\) và \(BD\).
-
D.
Giao điểm của \(MN\) và \(\left( {SBD} \right)\) là giao điểm của \(MN\) và \(BD\,.\)
Tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\)
- Để chứng minh A là giao điểm của đường thẳng d và mp \(\left( \alpha \right)\), ta phải chứng minh \(\left\{ \begin{array}{l}A \in d\\A \in \left( \alpha \right)\end{array} \right.\)
Khi đó \(\left\{ A \right\} = d \cap \left( \alpha \right)\)
Phương pháp tổng quát:
Bước 1: Tìm một mặt phẳng phụ \(\left( \beta \right)\) chứa d
Bước 2: Tìm giao tuyến \(\Delta = \left( \alpha \right) \cap \left( \beta \right)\)
Bước 3: Trong \(\left( \beta \right)\) có \(\Delta \cap d = \left\{ M \right\}\)
Vậy \(\left( \alpha \right) \cap d = \left\{ M \right\}\)
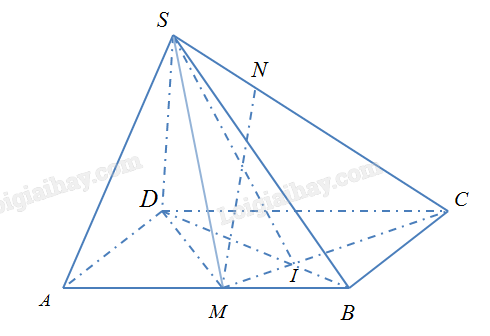
Ta thấy, \(MN \subset (SMC)\)ta tìm giao tuyến của (SMC) và (SBD)
Dễ dàng tìm được \((SMC) \cap \left( {SBD} \right) = SI\) trong đó \(I\) là giao điểm của \(CM\) và \(BD\).
\( \Rightarrow \) Giao điểm của \(MN\) và \(\left( {SBD} \right)\) là giao điểm của \(MN\) và \(SI\).
Đáp án : C







