Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K lần lượt là trung điểm hai đoạn thẳng AD và BC. IK là giao tuyến của cặp mặt phẳng nào sau đây?
-
A.
(IBC) và (KBD).
-
B.
(IBC) và (KCD).
-
C.
(IBC) và (KAD).
-
D.
(ABI) và (KAD).
Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Tìm hai điểm chung phân biệt của hai mặt phẳng đó.
\(\left\{ \begin{array}{l}A \in \left( \alpha \right)\\A \in \left( \beta \right)\end{array} \right. \Rightarrow A \in \left( \alpha \right) \cap \left( \beta \right)\)
\(\left\{ \begin{array}{l}B \in \left( \alpha \right)\\B \in \left( \beta \right)\end{array} \right. \Rightarrow B \in \left( a \right) \cap \left( \beta \right)\)
\( \Rightarrow AB = \left( \alpha \right) \cap \left( \beta \right)\).
Chú ý. Hai đường thẳng phân biệt cắt nhau khi và chỉ khi chúng cùng nằm trên một mặt phẳng và không song song với nhau.
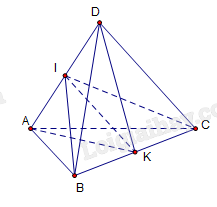
Ta có :
\(\left\{ \begin{array}{l}I \in AD \subset \left( {KAD} \right)\\I \in \left( {IBC} \right)\end{array} \right.\) \( \Rightarrow I\) là điểm chung thứ nhất của hai mặt phẳng \(\left( {IBC} \right)\) và \(\left( {KAD} \right)\).
\(\left\{ \begin{array}{l}K \in BC \subset \left( {IBC} \right)\\K \in \left( {KAD} \right)\end{array} \right.\)\( \Rightarrow K\) là điểm chung thứ hai của hai mặt phẳng \(\left( {IBC} \right)\) và \(\left( {KAD} \right)\).
Vậy \(\left( {IBC} \right) \cap \left( {KAD} \right) = IK\).
Đáp án : C

Các bài tập cùng chuyên đề
Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.
a) Xác định giao điểm của mp (E,d) với các cạnh SB, SD của hình chóp.
b) Xác định giao tuyến của mp (E,d) với các mặt của hình chóp.
Cho hình tứ diện ABCD. Trên các cạnh AC, BC, BD lần lượt lấy các điểm M, N, P sao cho AM = CM, BN = CN, BP = 2DP.
a) Xác định giao tuyến của đường thẳng CD và mặt phẳng (MNP)
b) Xác định giao tuyến của hai mặt phẳng (ACD) và (MNP).
Tại các nhà hàng, khách sạn, nhân viên phụ vụ bàn thường xuyên phải bưng bê nhiều khay, đĩa đồ ăn khác nhau. Một trong những nguyên tắc nhân viên cần nhớ là khay phải được bưng bằng ít nhất 3 ngón tay. Hãy giải thích tại sao?

Bàn cắt giấy là một dụng cụ được sử dụng thường xuyên ở các cửa hàng photo – copy. Bàn cắt giấy gồm hai phần chính: phần bàn hình chữ nhật có chia kích thước giấy và phần dao cắt có một đầu được cố định vào bàn. Hãy giải thích tại sao khi sử dụng bàn cắt giấy thì các đường cắt luôn là đường thẳng.

Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD)
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.
a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI)
b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: \(\frac{{GM}}{{GA}} = \frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và \(\frac{{GP}}{{GC}} = \frac{{GQ}}{{GD}} = \frac{1}{3}\)
Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\).
a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\).
b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\).
a) Tìm giao điểm \(I\) của đường thẳng \(AM\) và mặt phẳng \(\left( {SBD} \right)\). Chứng minh \(IA = 2IM\).
b) Tìm giao điểm \(E\) của đường thẳng \(SD\) và mặt phẳng \(\left( {ABM} \right)\).
c) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M,N\) lần lượt là trung điểm của \(SB,SD\); \(P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).
a) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \(\left( {MNP} \right)\).
b) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \(\left( {MNP} \right)\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(A{\rm{D}}\). Chứng minh \(I,J,K\) thẳng hàng.
Cho tứ diện \(ABCD\). Gọi \(E,F,G\) lần lượt là ba điểm trên ba cạnh \(AB,AC,BD\) sao cho \(EF\) cắt \(BC\) tại \(I\left( {I \ne C} \right)\), \(EG\) cắt \(A{\rm{D}}\) tại \(H\left( {H \ne D} \right)\).
a) Tìm giao tuyến của các mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\); \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\).
b) Chứng minh ba đường thẳng \(CD,IG,HF\) cùng đi qua một điểm.
Thước laser phát ra tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41). Giải thích tại sao các thước kẻ laser lại giúp người thợ xây dựng kẻ được đường thẳng trên tường hoặc sàn nhà.

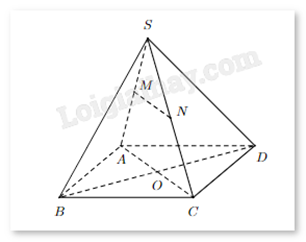
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC. Đường thẳng nào sau đây không thuộc mặt phẳng (SAC)?
-
A.
SA
-
B.
MN
-
C.
AC
-
D.
BO
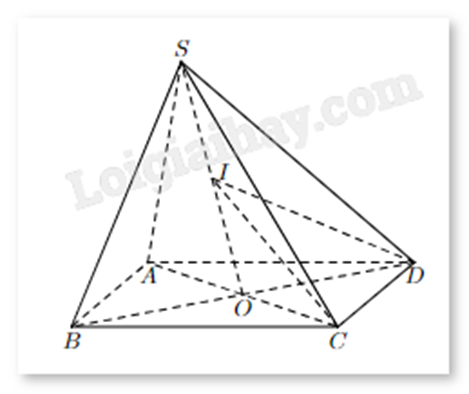
Cho hình chóp S.ABCD đáy là hình bình hành, cạnh AB = 6 cm, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng (ICD) cắt SA, SB lần lượt tại M, N. Độ dài MN là?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M nằm trên cạnh AD (giữa A và D) sao cho AD = 3MD. Một mặt phẳng \((\alpha )\) đi qua M, song song với CD và SA, cắt BC, SC, SD lần lượt tại N, P, Q. Với cạnh CD = 9 (cm) thì độ dài đoạn PQ là bao nhiêu?
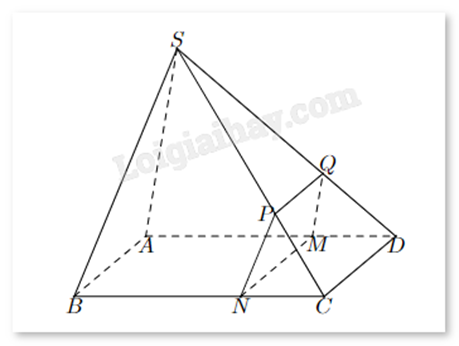
Cho hình chóp \(S.ABCD\) (hình vẽ). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Điểm \(O\) không thuộc mặt phẳng nào sau đây?
-
A.
\(\left( {SAC} \right)\)
-
B.
\(\left( {SBD} \right)\)
-
C.
\(\left( {SAB} \right)\)
-
D.
\(\left( {ABCD} \right)\)
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) trong không gian. Có bao nhiêu vị trí tương đối của \(a\) và \(\left( P \right)\)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Cho hình chóp \(A.BCD\) có \(G\) là trọng tâm tam giác \(BCD\). Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\) là
-
A.
\(AN\) với \(N\) là trung điểm của \(CD\)
-
B.
\(AM\) với \(M\) là trung điểm của \(AB\)
-
C.
\(AH\) với \(H\) là hình chiếu của \(B\) trên \(CD\)
-
D.
\(AK\) với \(K\) là hình chiếu của \(C\) trên \(BD\)
Cho bốn điểm \(A,\,B,\,C,\,D\) không cùng nằm trong một mặt phẳng. Trên \(AB,\,AD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(MN\) cắt \(BD\) tại \(I\). Điểm \(I\) không thuộc mặt phẳng nào sao đây?
-
A.
\(\left( {BCD} \right)\)
-
B.
\(\left( {ABD} \right)\)
-
C.
\(\left( {CMN} \right)\)
-
D.
\(\left( {ACD} \right)\)
Cho tứ diện \(ABCD\) có \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(AD\). Gọi \(G\) là trọng tâm của tam giác \(BCD\). Gọi \(I\) là giao điểm của \(NG\) với mặt phẳng \(\left( {ABC} \right)\). Khẳng định nào sau đây đúng?
-
A.
\(I \in AM\)
-
B.
\(I \in BC\)
-
C.
\(I \in AC\)
-
D.
\(I \in AB\)
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AD,BC\), điểm \(G\) là trọng tâm của tam giác \(BCD\). Giao điểm của đường thẳng \(MG\) với mặt phẳng \(\left( {ABC} \right)\) là
-
A.
Giao điểm của \(MG\) và \(BC\)
-
B.
Giao điểm của \(MG\) và \(AC\)
-
C.
Giao điểm của \(MG\) và \(AN\)
-
D.
Giao điểm của \(MG\) và \(AB\)
Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(d \not\subset \left( \alpha \right)\). Khẳng định nào sau đây là sai?
-
A.
Nếu \(d\,{\rm{//}}\,\left( \alpha \right)\) thì trong \(\left( \alpha \right)\) tồn tại đường thẳng \(\Delta \) sao cho \(\Delta \,{\rm{//}}\,d\)
-
B.
Nếu \(d\,{\rm{//}}\,\left( \alpha \right)\) và \(b \subset \left( \alpha \right)\) thì \(b\,{\rm{//}}\,d\)
-
C.
Nếu \(d \cap \left( \alpha \right) = A\) và \(d' \subset \left( \alpha \right)\) thì \(d\) và \(d'\) hoặc cắt nhau hoặc chéo nhau
-
D.
Nếu \(d\,{\rm{//}}\,c\,;\,\,c \subset \left( \alpha \right)\) thì \(d\,{\rm{//}}\,\left( \alpha \right)\)
Cho tứ diện \(ABCD.\) Gọi \(E\) và \(F\) lần lượt là trung điểm của \(AB\) và \(CD\); \(G\) là trọng tâm tam giác \(BCD.\) Giao điểm của đường thẳng \(EG\) và mặt phẳng \(\left( {ACD} \right)\) là
-
A.
Điểm \(F\)
-
B.
Giao điểm của đường thẳng \(EG\) và \(AF\)
-
C.
Giao điểm của đường thẳng \(EG\) và \(AC\)
-
D.
Giao điểm của đường thẳng \(EG\) và \(CD\)
Gọi $G$ là trọng tâm tứ diện $ABCD$. Gọi $A'$ là trọng tâm của tam giác $BCD$. Tính tỉ số $\frac{{GA}}{{GA'}}$.
-
A.
2
-
B.
3
-
C.
$\frac{1}{3}$
-
D.
$\frac{1}{2}$
Trong mặt phẳng (P), cho hình bình hành ABCD tâm O, ngoài mặt phẳng (P) cho một điểm S.
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
Cho tứ diện $ABCD$. Khẳng định nào sau đây là đúng?
-
A.
$AB$ và $CD$ cắt nhau.
-
B.
Bốn điểm $A,\,\,B,\,\,C,\,\,D$ không đồng phẳng.
-
C.
$AC$ và $BD$ cắt nhau.
-
D.
Bốn điểm $A,\,\,B,\,\,C,\,\,D$ thẳng hàng.
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình bình hành và $N$ là trung điểm của cạnh $SA$.
a) Tìm giao điểm của $AC$ và mặt phẳng $(SBD)$.
b) Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng $(NBC)$. Thiết diện là hình gì?
Cho bốn điểm $A,\,\,B,\,\,C,\,\,D$ không đồng phẳng. Gọi $M,\,\,N$ lần lượt là trung điểm của $AC$ và $BC$. Trên đoạn $BD$ lấy điểm $P$ sao cho $BP = 2PD$. Giao điểm của đường thẳng $CD$ và mặt phẳng $\left( {MNP} \right)$ là giao điểm của
-
A.
$CD$ và $NP$.
-
B.
$CD$ và $MN$.
-
C.
$CD$ và $MP$.
-
D.
$CD$ và $AP$.
Cho hình chóp S.ABCD có đáy ABCD là hình thang (hai đáy AB > CD). Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao điểm P của SC và mặt phẳng (ADN).
b) Biết AN cắt DP tại I. Chứng minh SI // AB. Tứ giác SABI là hình gì?







Danh sách bình luận