Cho hình chóp S.ABCD có đáy là hình thang ABCD (AD // BC). Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:
-
A.
SP với P là giao điểm của AB và CD
-
B.
SI với I là giao điểm của AC và BM
-
C.
SO với O là giao điểm của AC và BD
-
D.
SJ với J là giao điểm của AM và BD
Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Tìm hai điểm chung phân biệt của hai mặt phẳng đó.
\(\left\{ \begin{array}{l}A \in \left( \alpha \right)\\A \in \left( \beta \right)\end{array} \right. \Rightarrow A \in \left( \alpha \right) \cap \left( \beta \right)\)
\(\left\{ \begin{array}{l}B \in \left( \alpha \right)\\B \in \left( \beta \right)\end{array} \right. \Rightarrow B \in \left( a \right) \cap \left( \beta \right)\)
\( \Rightarrow AB = \left( \alpha \right) \cap \left( \beta \right)\).
Chú ý. Hai đường thẳng phân biệt cắt nhau khi và chỉ khi chúng cùng nằm trên một mặt phẳng và không song song với nhau.
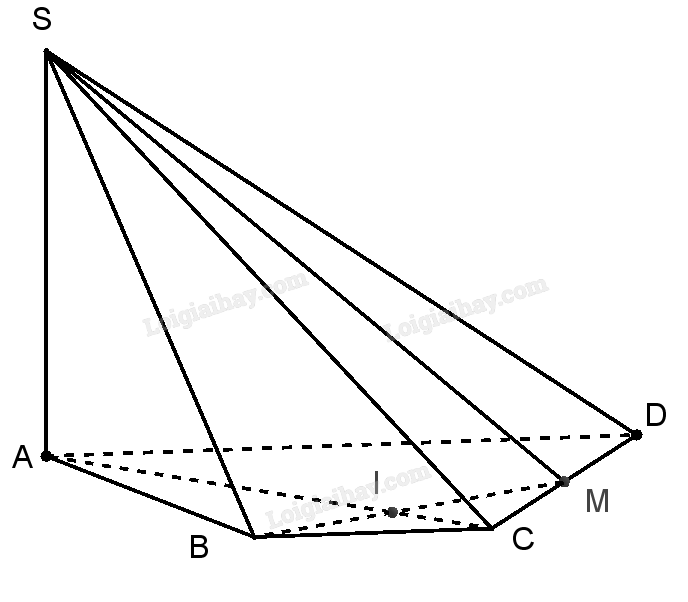
Ta có: \(AC \cap BM = I \Rightarrow I \in (SAC) \cap (SBM)\).
Lại có: \(S \in (SAC) \cap (SBM)\).
\( \Rightarrow (SAC) \cap (SBM) = SI\).
Vậy giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\) là \(SI\) với \(I\) là giao điểm của \(AC\) và \(BM\).
Đáp án : B
