Tổng lượng mưa trong tháng 8 đo được tại một trạm quan trắc đặt tại Vũng Tàu từ năm 2002 đến năm 2020 được ghi lại như dưới đây (đơn vị: mm):

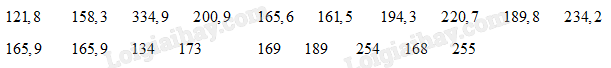
(Nguồn: Tổng cục Thống kê)  

Hoàn thiện bảng tần số ghép nhóm theo mẫu sau và tìm tứ phân vị thứ hai của mẫu số liệu góp nhóm đó

Công thức xác định tứ phân vị của mẫu số liệu ghép nhóm

Tứ phận vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu là \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.

Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất;

\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất;

\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).

Khi đó  \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).

Tương tự, để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba;

\({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba;

\(C = {n_1} + {n_2} + ... + {n_{j - 1}}\).

Khi đó \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\).