Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
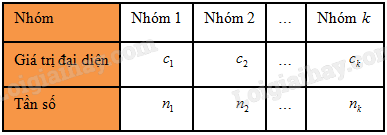
Đặt \(n = {n_1} + {n_2} + \ldots + {n_k}\).
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\mathop x\limits^ - \), được tính theo công thức nào?
-
A.
\(\mathop x\limits^ - = \frac{{{n_1}{c_1} + {n_2}{c_2} + \ldots + {n_k}{c_k}}}{n}\).
-
B.
\(\mathop x\limits^ - = \frac{{{n_1}{c_1} + {n_2}{c_2} + \ldots + {n_k}{c_k}}}{{2n}}\).
-
C.
\(\mathop x\limits^ - = \frac{{n_{_1}^2{c_1} + n_{_2}^2{c_2} + \ldots + n_{_k}^2{c_k}}}{n}\).
-
D.
\(\mathop x\limits^ - = \frac{{{n_1}{c_1} + {n_2}{c_2} + \ldots + {n_k}{c_k}}}{{\sqrt n }}\)
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
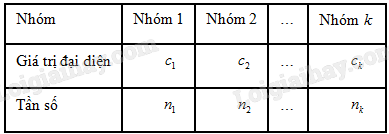
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\mathop x\limits^ - \), được tính như sau:
\(\mathop x\limits^ - = \frac{{{n_1}{c_1} + {n_2}{c_2} + \ldots + {n_k}{c_k}}}{n}\)
trong đó \(n = {n_1} + {n_2} + \ldots + {n_k}\).
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
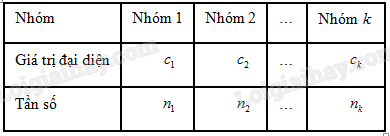
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\mathop x\limits^ - \), được tính như sau:
\(\mathop x\limits^ - = \frac{{{n_1}{c_1} + {n_2}{c_2} + \ldots + {n_k}{c_k}}}{n}\)
trong đó \(n = {n_1} + {n_2} + \ldots + {n_k}\).
Đáp án : A







