Đề bài
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
-
A.
Hình chữ nhật
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Phương pháp giải
Chứng minh tứ giác MNED có MN // ED, MN = ED nên tứ giác MNED là hình bình hành
Lời giải của GV Loigiaihay.com
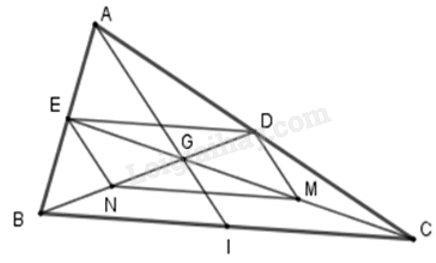
Xét tam giác ABC : ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) (1)
+ Xét tam giác GBC có : MN // BC; \(MN = \frac{1}{2}BC\) (2)
Từ (1), (2) ⇒ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Đáp án : B








Danh sách bình luận