Tìm tập nghiệm của phương trình \(\tan 3x + \tan x = 0\).
-
A.
\(\left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\).
-
B.
\(\left\{ {\frac{{k\pi }}{4}} \right\}\).
-
C.
\(\left\{ {k\pi ;\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\).
-
D.
\(\left\{ {k\pi ;\frac{\pi }{4} + k\pi } \right\}\).
Biến đổi phương trình về dạng cơ bản bằng cách sử dụng công thức lượng giác
\(\tan \left( { - x} \right) = - \tan x\)
Điều kiện: \(\left\{ \begin{array}{l}\cos 3x \ne 0\\\cos x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{6} + \frac{{k\pi }}{3}\\x \ne \frac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow x \ne \frac{\pi }{6} + \frac{{k\pi }}{3},\,\,k \in \mathbb{Z}\)
\(\tan 3x + \tan x = 0 \Leftrightarrow \tan 3x = \tan \left( { - x} \right) \Leftrightarrow 3x = - x + k\pi \Leftrightarrow x = \frac{{k\pi }}{4},\,\,k \in \mathbb{Z}\)
Kết hợp điều kiện suy ra nghiệm của phương trình là \(x = k\pi ;\,\,x = \frac{\pi }{4} + \frac{{k\pi }}{2}\).
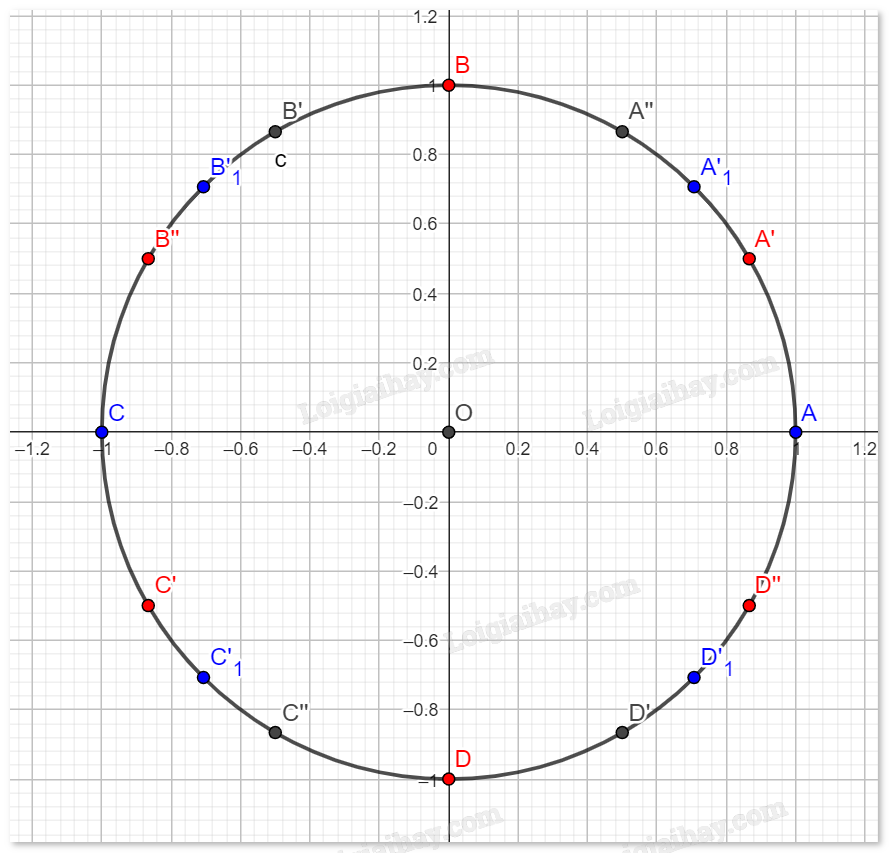
Cách kết hợp điều kiện để tìm nghiệm: Sử dụng đường tròn lượng giác.
Điểm màu đỏ đại diện cho các giá trị bị loại khi tìm điều kiện xác định \(x \ne \frac{\pi }{6} + \frac{{k\pi }}{3},\,\,k \in \mathbb{Z}\).
Điểm màu xanh là các giá trị \(x = \frac{{k\pi }}{4}\) thỏa mãn điều kiện. Ta biểu diễn lại các điểm này là \(x = k\pi ;\,\,x = \frac{\pi }{4} + \frac{{k\pi }}{2}\).
Vị trí A; C là \(x = k\pi \).
Vị trí \({A_1}';{B_1}';{C_1}';{D_1}'\) là \(x = \frac{\pi }{4} + \frac{{k\pi }}{2}\).
Đáp án : C








Danh sách bình luận