Hàm số nào đồng biến trên khoảng \(\left( { - \frac{\pi }{3};\frac{\pi }{6}} \right)\):
-
A.
\(y = \cos x\).
-
B.
\(y = \cot 2x\).
-
C.
\(y = \sin x\).
-
D.
\(y = {\rm{cos}}2x\)
Phương pháp 1
Hàm số \(y = \sin x:\)* Đồng biến trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\,\,\frac{\pi }{2} + k2\pi } \right),\,k \in \mathbb{Z}.\)
* Nghịch biến trên các khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\,\,\frac{{3\pi }}{2} + k2\pi } \right),\,k \in \mathbb{Z}.\)
Hàm số \(y = \cos x:\)
* Đồng biến trên các khoảng \(\left( { - \pi + k2\pi ;\,\,k2\pi } \right),\,k \in \mathbb{Z}.\)
* Nghịch biến trên các khoảng \(\left( {k2\pi ;\,\,\pi + k2\pi } \right),\,k \in \mathbb{Z}.\)
Hàm số \(y = \tan x\) đồng biến trên các khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\,\,\frac{\pi }{2} + k\pi } \right),\,k \in \mathbb{Z}.\)
Hàm số \(y = \cot x\) nghịch biến trên các khoảng \(\left( {k\pi ;\,\,\pi + k\pi } \right),\,k \in \mathbb{Z}.\)
Phương pháp 2: sử dụng đường tròn lượng giác:
Vẽ vòng tròn lượng giác.Biểu diễn các cung lượng giác trên vòng tròn lượng giác.
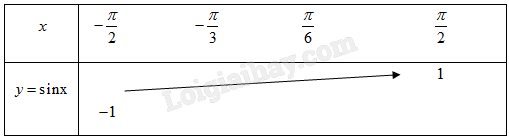
Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) mà \(\left( { - \frac{\pi }{3};\frac{\pi }{6}} \right) \subset \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), ta thấy trên khoảng \(\left( { - \frac{\pi }{3};\frac{\pi }{6}} \right)\) hàm \(y = \sin x\) đồng biến.
Đáp án : C
