Phương trình \(\sin x = \frac{x}{{2019}}\) có bao nhiêu nghiệm thực?
-
A.
\(1290\).
-
B.
\(1287\).
-
C.
\(1289\).
-
D.
\(1288\).
Nhận xét: Số nghiệm phương trình \(f\left( x \right) = g\left( x \right)\) đúng bằng số điểm chung của hai đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right)\)
Vẽ đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right)\) để tìm số điểm chung của chúng rồi kết luận số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\)
Đk: \( - 2019 \le x \le 2019\)
Nhận xét \(x = 0\) là nghiệm của phương trình.
Nếu \(x = {x_0}\) là nghiệm của phương trình thì \(x = - {x_0}\) cũng là nghiệm của phương trình
Ta xét nghiệm của phương trình trên đoạn \(\left[ {0;2019} \right]\). Vẽ đồ thị của hàm số \(y = \sin x\)và \(y = \frac{x}{{2019}}\). Ta thấy
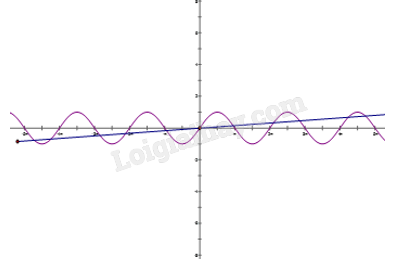
Trên đoạn \(\left[ {0;2\pi } \right]\) phương trình có hai nghiệm phân biệt
Trên nửa khoảng \(\left( {2\pi ;4\pi } \right]\) phương trình có hai nghiệm phân biệt
Trên nửa khoảng \(\left( {4\pi ;6\pi } \right]\) phương trình có hai nghiệm phân biệt
…
Trên nửa khoảng \(\left( {640\pi ;642\pi } \right]\) phương trình có hai nghiệm phân biệt
Trên nửa khoảng \(\left( {642\pi ;2019} \right]\) phương trình có hai nghiệm phân biệt.
Như vậy trên đoạn \(\left[ {0;2019} \right]\) phương trình có một nghiệm \(x = 0\) và \(321{\rm{ x 2 + 1 = 643}}\) nghiệm dương phân biệt. Mà do \(x = {x_0}\) là nghiệm của phương trình thì \(x = - {x_0}\) cũng là nghiệm của phương trình nên trên nửa khoảng \(\left[ { - 2019;0} \right)\) phương trình cũng có \(643\) nghiệm âm phân biệt.
Do đó trên đoạn \(\left[ { - 2019;2019} \right]\) phương trình có số nghiệm thực là \({\rm{643 x 2 + 1 = 1287}}\) nghiệm
Vậy số nghiệm thực của phương trình đã cho là \(1287\)nghiệm.
Đáp án : B
Các bài tập cùng chuyên đề
Tập xác định của hàm số \(y = \tan \,\left( {2x - \frac{\pi }{3}} \right)\) là
-
A.
\(D = \left\{ {x \in \mathbb{R}|x \ne \frac{\pi }{6} + \frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\).
-
B.
\(D = \left\{ {x \in \mathbb{R}|x \ne \frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}} \right\}\).
-
C.
\(D = \left\{ {x \in \mathbb{R}|x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
-
D.
\(D = \left\{ {x \in \mathbb{R}|x \ne \frac{{5\pi }}{{12}} + k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
Hàm số \(y = \cot {\rm{2x}}\)có tập xác định là
-
A.
\(k\pi \)
-
B.
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi ;k \in \mathbb{Z}} \right\}\)
-
C.
\(\mathbb{R}\backslash \left\{ {k\frac{\pi }{2};k \in \mathbb{Z}} \right\}\)
-
D.
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2};k \in \mathbb{Z}} \right\}\)
Hàm số \(y = \cos x\) đồng biến trên đoạn nào dưới đây:
-
A.
\(\left[ {0;\frac{\pi }{2}} \right]\).
-
B.
\(\left[ {\pi ;2\pi } \right]\).
-
C.
\(\left[ { - \pi ;\pi } \right]\).
-
D.
\(\left[ {0;\pi } \right]\).
Tìm hàm số chẵn trong các hàm số sau
-
A.
\(y = \sin x\).
-
B.
\(y = \cot x\).
-
C.
\(y = \cos x\).
-
D.
\(y = \tan x\).
Khẳng định nào sau đây là sai về tính tuần hoàn và chu kì của các hàm số?
-
A.
Hàm số \(y = \sin x\) là hàm số tuần hoàn chu kì \(2\pi .\)
-
B.
Hàm số \(y = \cos x\) là hàm số tuần hoàn chu kì \(\pi .\)
-
C.
Hàm số \(y = \tan x\) là hàm số tuần hoàn chu kì \(\pi .\)
-
D.
Hàm số \(y = \cot x\) là hàm số tuần hoàn chu kì \(\pi .\)
Tập xác định của hàm số \(y = \cot \left( {x + \frac{\pi }{6}} \right) + \sqrt {\frac{{1 + \cos x}}{{1 - \cos x}}} \) là:
-
A.
\(D = R\backslash \left\{ { - \frac{\pi }{6} + k2\pi |k \in Z} \right\}\).
-
B.
\(D = R\backslash \left\{ {\frac{{5\pi }}{6} + k\pi ,k2\pi |k \in Z} \right\}\).
-
C.
\(D = R\backslash \left\{ {k2\pi |k \in Z} \right\}\).
-
D.
\(D = R\backslash \left\{ { - \frac{\pi }{6} + k\pi |k \in Z} \right\}\).
Tìm tập xác định của hàm số \(y = \sqrt {\frac{{1 - \cos 3x}}{{1 + \sin 4x}}} \)
-
A.
\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{8} + k\frac{\pi }{2},{\rm{ }}k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ { - \frac{{3\pi }}{8} + k\frac{\pi }{2},{\rm{ }}k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{4} + k\frac{\pi }{2},{\rm{ }}k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{6} + k\frac{\pi }{2},{\rm{ }}k \in \mathbb{Z}} \right\}\)
Tìm tất cả giá trị \(m\) để hàm số\(y = \sqrt {{m^2} - \sin x} \) hàm số có tập xác định là \(\mathbb{R}.\)
-
A.
\(m > 1\).
-
B.
\(m \le - 1;m \ge 1\).
-
C.
\( - 1 \le m \le 1\).
-
D.
\(m \ge 1\).
Tập xác định của hàm số \(y = \frac{{3\tan x - 5}}{{1 - {{\sin }^2}x}}\) là:
-
A.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\pi + k\pi |k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\)
Hình nào sau đây là đồ thị hàm số \(y = \cos x + 2\)?
-
A.
-
B.
-
C.
-
D.
Tìm chu kì của hàm số \(f\left( x \right) = \sin \frac{x}{2} + 2\cos \frac{{3x}}{2}\).
-
A.
\(5\pi \).
-
B.
\(\frac{\pi }{2}\).
-
C.
\(4\pi \).
-
D.
\(2\pi \)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sin x\) trên đoạn \(\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]\) lần lượt là:
-
A.
\( - \frac{1}{2}\); \( - \frac{{\sqrt 3 }}{2}\).
-
B.
\( - \frac{{\sqrt 3 }}{2}\); \( - 1\).
-
C.
\( - \frac{{\sqrt 3 }}{2}\); \( - 2\).
-
D.
\( - \frac{{\sqrt 2 }}{2}\); \( - \frac{{\sqrt 3 }}{2}\).
Hàm số \(y = \sin x + \frac{1}{2}\sin 2x + \frac{1}{3}\sin 3x\) tuần hoàn với chu kì?
-
A.
\(2\pi .\)
-
B.
\(\pi .\)
-
C.
\(4\pi .\)
-
D.
\(6\pi .\)
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
-
A.
\(y = \frac{1}{{{{\sin }^3}x}}.\)
-
B.
\(y = \sin \left( {x + \frac{\pi }{4}} \right).\)
-
C.
\(y = \sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right).\)
-
D.
\(y = \sqrt {\sin 2x} .\)
Cho hàm số \({\rm{f}}\left( x \right) = 2{x^2} - 4x + 1\). Tìm giá trị lớn nhất của hàm số \({\rm{y = f}}\left( {\sin x} \right);x \in \left[ { - \frac{\pi }{2};\frac{\pi }{6}} \right]\)
-
A.
\(6\).
-
B.
\(\frac{{13}}{2}\).
-
C.
\(\frac{{11}}{2}\).
-
D.
\(\frac{9}{2}\).
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h\((m)\) của con kênh tính theo thời gian \(t\) (giờ) trong một ngày được cho bởi công thức: \(h = \frac{1}{2}\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 3\). Thời điểm mực nước của kênh cao nhất là:
-
A.
\(t = 15\)
-
B.
\(t = 16\)
-
C.
\(t = 13\)
-
D.
\(t = 14\)
Tìm \(m\) để bất phương trình \(\frac{{3\sin 2x + \cos 2x}}{{\sin 2x + 4{{\cos }^2}x + 1}} \le m + 1\) đúng với mọi \(x \in \mathbb{R}\).
-
A.
\(m \ge \frac{{3\sqrt 5 }}{4}\).
-
B.
\(m \ge \frac{{3\sqrt 5 + 9}}{4}\).
-
C.
\(m \ge \frac{{\sqrt {65} - 9}}{4}\).
-
D.
\(m \ge \frac{{3\sqrt 5 - 9}}{4}\).
Số giờ có ánh sáng của một thành phố\(A\) trong ngày thứ \(t\) của năm \(2017\)được cho bởi một hàm số \(y = 4\sin \left| {\frac{\pi }{{178}}\left( {t - 60} \right)} \right| + 10\), với \(t \in Z\) và \(0 < t \le 365\). Vào ngày nào trong năm thì thành phố \(A\) có nhiều giờ ánh sáng mặt trời nhất ?.
-
A.
\(28\) tháng \(5\).
-
B.
\(29\) tháng \(5\).
-
C.
\(30\) tháng \(5\).
-
D.
\(31\) tháng \(5\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau
Số nghiệm thuộc đoạn \(\left[ { - \frac{{3\pi }}{2};2\pi } \right]\) của phương trình \(3f\left( {\cos 2x} \right) - 4 = 0\) là
-
A.
\(14\).
-
B.
\(3\).
-
C.
\(11\).
-
D.
\(16\).
