Cho góc α thỏa mãn \(\frac{\pi }{2} < \alpha < \pi \). Xét các mệnh đề sau:
I. \(c{\rm{os(}}\frac{\pi }{2} - \alpha ){\rm{ > 0}}\).
II. \({\rm{sin(}}\frac{\pi }{2} - \alpha ){\rm{ > 0}}\).
III. \({\rm{tan(}}\frac{\pi }{2} - \alpha ){\rm{ > 0}}\).
Mệnh đề nào sai ?
-
A.
Chỉ I
-
B.
Chỉ II
-
C.
Chỉ II và III
-
D.
Cả I, II và III
Xét điểm biểu diễn của góc \(\frac{\pi }{2} - \alpha \) thuộc góc phần tư thứ mấy để suy ra dấu của các giá trị lượng giác.
\(\frac{\pi }{2} < \alpha < \pi \Leftrightarrow - \frac{\pi }{2} < \frac{\pi }{2} - \alpha < 0\) nên điểm biểu diễn của góc \(\frac{\pi }{2} - \alpha \) thuộc góc phần tư thứ IV.
\( \Rightarrow \) Chỉ I đúng; II và III sai.
Đáp án : C
Ta cần xét góc \(\frac{\pi }{2} - \alpha \) thay vì góc \( \alpha\).
Điểm biểu diễn của góc \( \alpha\) thuộc góc phần tư thứ II.
Điểm biểu diễn của góc \(\frac{\pi }{2} - \alpha \) thuộc góc phần tư thứ IV.
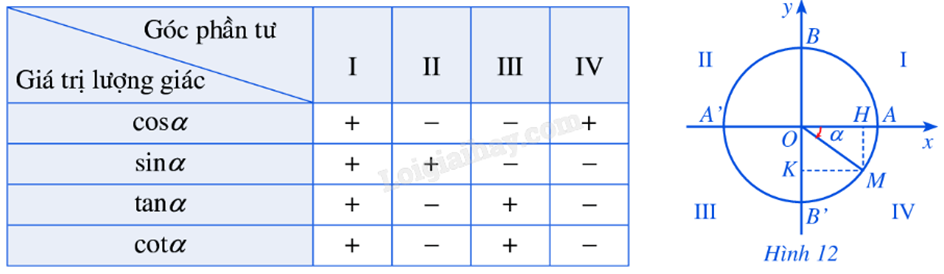
Dấu của các giá trị lượng giác:
