Đề bài
Cho góc hình học \(\widehat {uOv} = {45^0}\). Xác định số đo của góc lượng giác (Ou,Ov) trong hình dưới đây:
-
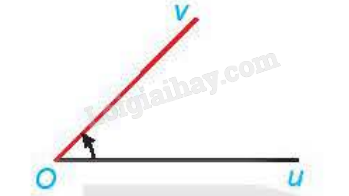
A.
\({45^0} + k{360^0}(k \in Z)\)
-
B.
\( - {45^0} + k{360^0}(k \in Z)\)
-
C.
\({135^0} + k{360^0}(k \in Z)\)
-
D.
\( - {135^0} + k{360^0}(k \in Z)\)
Phương pháp giải
Số đo của góc lượng giác tia đầu Ou, tia cuối Ov là:
sđ (Ou,Ov) = \({a^0} + k{360^0}(k \in Z)\)
Xác định dấu của a:
- Nếu Ou quay cùng chiều kim đồng hồ thì a mang dấu ấm.
- Nếu Ou quay ngược chiều kim đồng hồ thì a mang dấu dương.
Lời giải của GV Loigiaihay.com
Do \(\widehat {uOv} = {45^0}\) và tia Ou quay ngược chiều kim đồng hồ nên
sđ (Ou,Ov) = \({45^0} + k{360^0}(k \in Z)\)
Đáp án : A
