Cho tứ giác ABCD có \(\widehat A = {80^o}\) . Tổng số đo các góc ngoài đỉnh B, C, D bằng:

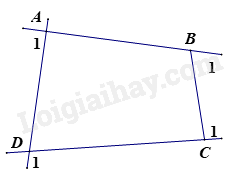
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .

Ta có: \(\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - {80^o} = {100^o}\)

Khi đó ta có:

\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)

Suy ra:

\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\\ \Rightarrow \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {360^o} - \widehat {{A_1}} = {360^o} - {100^o} = {260^o}\end{array}\)