Đề bài
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
-
A.
\({113^o}\)
-
B.
\({107^o}\)
-
C.
\({58^o}\)
-
D.
\({83^o}\)
Phương pháp giải
Tính góc D trong tứ giác ABCD. Từ đó góc ngoài tại đỉnh D bằng \({180^o}\) trừ đi góc D trong tứ giác ABCD.
Góc ngoài và góc trong tứ giác tại một đỉnh là hai góc kề bù.
Lời giải của GV Loigiaihay.com
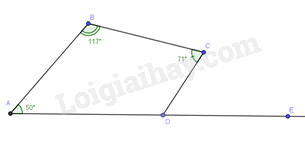
\(\widehat {C{{D}}E}\) là góc ngoài đỉnh D. Tứ giác ABCD có:
\(\begin{array}{l}\widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right)\\\widehat D = {360^o} - \left( {{{50}^o} + {{117}^o} + {{71}^o}} \right)\\\widehat D = {122^o}\end{array}\)
Vì \(\widehat {A{{D}}C}\) và \(\widehat {C{{D}}E}\) là hai góc kề bù nên:
\(\widehat {C{{D}}E} = {180^o} - \widehat D = {180^o} - {122^o} = {58^o}\)
Đáp án : C
