Đề bài
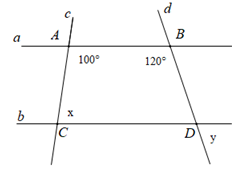
Cho hình vẽ dưới đây, biết \(a//b\). Tính \(x;y.\)
-
A.
\(x = 80^\circ ;y = 80^\circ .\)
-
B.
\(x = 60^\circ ;y = 80^\circ .\)
-
C.
\(x = 80^\circ ;y = 60^\circ .\)
-
D.
\(x = 60^\circ ;y = 60^\circ .\)
Phương pháp giải
Áp dụng tính chất hai đường thẳng song song để tính \(x.\)
Áp dụng tính chất hai góc đối đỉnh để tính \(y.\)
Lời giải của GV Loigiaihay.com
Vì \(a//b\) nên \(\widehat {BAC} + \widehat {ACD} = 180^\circ \) (hai góc trong cùng phía bù nhau)
Suy ra \(100^\circ + x = 180^\circ \Rightarrow x = 80^\circ \)
Tương tự ta có \(\widehat {ABD} + \widehat {CDB} = 180^\circ \Rightarrow \widehat {CDB} = 60^\circ \)
Suy ra \(y = \widehat {CDB} = 60^\circ \) (hai góc đổi đỉnh)
Vậy \(x = 80^\circ ;y = 60^\circ .\)
Đáp án : C
