Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
-
A.
$\widehat {x'Oy} = 135^\circ $
-
B.
$\widehat {x'Oy'} = 45^\circ $
-
C.
$\widehat {xOy'} = 135^\circ $
-
D.
$\widehat {x'Oy'} = 135^\circ $
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
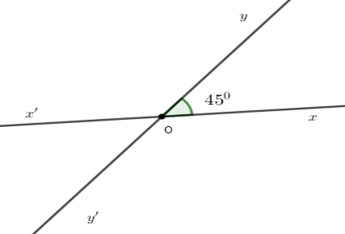
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Đáp án : D
Các bài tập cùng chuyên đề
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
Vẽ \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
Hai đường thẳng $xy$ và $x'y'$ cắt nhau tại $O.$ Biết \(\widehat {xOx'} = {70^o}\). $Ot$ là tia phân giác của góc xOx’. $Ot'$ là tia đối của tia $Ot.$ Tính số đo góc $yOt'.$
Cho đường thẳng $AB$ và điểm $O$ trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ $AB$ vẽ hai tia $OC$ và $OD$ sao cho \(\widehat {AOC} = \widehat {BOD} = {50^o}\). Trên nửa mặt phẳng bờ $AB$ không chứa tia $OD,$ vẽ tia $OE$ sao cho tia $OA$ là tia phân giác của góc $COE.$ Chọn câu đúng?
Cho \(\widehat {AOB} = 50^\circ \) , tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OC\). Trên nửa mặt phẳng bờ \(CD\) chứa tia \(OA\), vẽ tia \(OE\) sao cho \(\widehat {DOE} = 25^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {DOE}\).
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
