Một người nhìn hòn sỏi dưới đáy một bể nước thấy ảnh của nó dường như cách mặt nước một khoảng 120cm. Chiết suất của nước là n = \(\frac{4}{3}\). Độ sâu của bể nước là

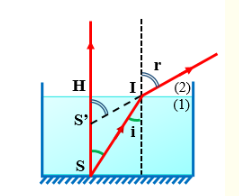
Gọi S là hòn sỏi dưới đáy bể, S’ là ảnh của S. Để ảnh rõ nét thì góc tới phải nhỏ

Ta có: \(\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{{{n_2}}}{{{n_1}}}(1)\)

Mà \(\tan i = \frac{{HI}}{{HS}};{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HS'}} \Rightarrow \frac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{HS'}}{{HS}}(2)\)

Vì góc tới nhỏ nên sini ≈ tani ≈i

Từ (1) và (2) ta được \(\frac{{{n_2}}}{{{n_1}}} = \frac{{HS'}}{{HS}} \Rightarrow HS = \frac{{{n_1}}}{{{n_2}}}HS' = 1,6m = 16dm\)