Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5},MN = 15\left( {cm} \right)\). Tính độ dài cạnh AC.
-
A.
AC = 21 (cm).
-
B.
AC = 37,5 (cm)
-
C.
AC = 52,5 (cm).
-
D.
AC = 25 (cm).
Dựa vào định lí Thales và định lý Thales đảo.
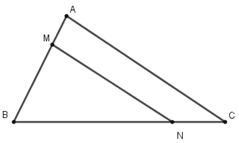
Ta có: \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5} \Rightarrow MN\parallel AC\)
\(\frac{{MA}}{{MB}} = \frac{2}{5},MA + MB = AB\)
\( \Rightarrow \frac{{MA}}{{AB}} = \frac{2}{7};\frac{{MB}}{{AB}} = \frac{5}{7}\)
Áp dụng định lý Talet trong tam giác ABC với MN//AC ta có:
\(\frac{{MB}}{{AB}} = \frac{{MN}}{{AC}} = \frac{5}{7}\)
\( \Rightarrow AC = \frac{{7MN}}{5} = \frac{{7.15}}{5} = 21\left( {cm} \right)\)
Đáp án : A
Các bài tập cùng chuyên đề
Viết tỉ số cặp đoạn thẳng có độ dài như sau: $AB = 4\,dm,CD = 20\,dm$
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:
Chọn câu trả lời đúng:
Cho hình thang $ABCD$ ($AB{\rm{//}}CD$),$O$ là giao điểm của $AC$ và$BD$ . Xét các khẳng định sau:
(I) \(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}}\) (II) \(\dfrac{{OB}}{{OC}} = \dfrac{{BC}}{{AD}}\)
Cho biết $M$ thuộc đoạn thẳng $AB$ thỏa mãn \(\dfrac{{AM}}{{MB}} = \dfrac{3}{8}\). Tính tỉ số \(\dfrac{{AM}}{{AB}}\) ?
Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) (II)\(AK = KB\)
(III) \(\dfrac{{AO}}{{AC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)
Chọn câu trả lời đúng: Cho hình bên, biết \(DE{\rm{//}}AC\), tìm \(x\) :
Cho tam giác $ABC$ có $AB = 9\,cm$, điểm $D$ thuộc cạnh $AB$ sao cho $AD = 6\,cm$. Kẻ $DE$ song song với $BC$ $\left( {E \in AC} \right)$, kẻ $EF$ song song với $CD$ $\left( {F \in AB} \right)$. Tính độ dài $AF$ .
Tính các độ dài $x,y$ trong hình bên:
Tìm giá trị của \(x\) trên hình vẽ.
Cho hình thang $ABCD$ $\left( {AB{\rm{//}}CD} \right)$ có $BC = 15\,cm$. Điểm $E$ thuộc cạnh $AD$ sao cho $\dfrac{{AE}}{{AD}} = \dfrac{1}{3}$. Qua $E$ kẻ đường thẳng song song với $CD$ , cắt $BC$ ở $F$ . Tính độ dài $BF$ .
Cho tam giác $ABC$ . Một đường thẳng song song với $BC$ cắt các cạnh $AB$ và $AC$ theo thứ tự ở $D$ và $E$ . Chọn câu đúng.
Cho tam giác $ABC$ , đường trung tuyến $AD$ . Gọi $K$ là điểm thuộc đoạn thẳng $AD$ sao cho $\dfrac{{AK}}{{KD}} = \dfrac{1}{2}$. Gọi $E$ là giao điểm của $BK$ và $AC$ . Tính tỉ số $\dfrac{{AE}}{{EC}}$.
Cho hình thang \(ABCD\)\(\left( {AB//CD} \right)\) có diện tích \(36\,c{m^2}\),\(AB = 4\,{\rm{cm,CD = 8}}\,{\rm{cm}}\). Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\).
Cho tứ giác \(ABCD\), lấy bất kỳ \(E \in BD\) . Qua \(E\) vẽ \(EF\) song song với \(AD\)( \(F\) thuộc \(AB\)), vẽ \(EG\) song song với \(DC\)(\(G\) thuộc\(BC\)). Chọn khẳng định sai.
Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
