Giá trị nhỏ nhất \({F_{\min }}\) của biểu thức \(F\left( {x;y} \right) = 4x + 3y\) trên miền xác định bởi hệ \(\,\left\{ \begin{array}{l}0 \le \,\,x\,\, \le \,\,10\\0\,\, \le \,\,y\,\, \le \,\,9\\2x\,\, + \,\,y\,\, \ge \,\,14\\2x\,\, + \,\,5y\,\, \ge \,\,30\end{array} \right.\) là

Trong mặt phẳng tọa độ \(Oxy\), vẽ các đường thẳng

\({d_1}:2x + y - 14 = 0,{d_2}:2x + 5y - 30 = 0,\Delta :y = 9,\Delta ':x = 10\).

Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (tứ giác \(ABCD\) kể cả biên) tô màu như hình vẽ.

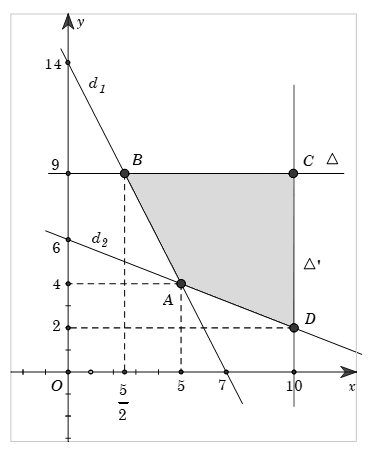
Xét các đỉnh của miền khép kín tạo bởi hệ là

\(\begin{array}{l}A\left( {5;4} \right),{\rm{ }}B\left( {\frac{5}{2};9} \right),{\rm{ }}C\left( {10;9} \right),{\rm{ }}D\left( {10;2} \right).\end{array}\)

Thay tọa độ từng điểm vào F(x;y) = 4x + 3y để tìm giá trị F nhỏ nhất:

\(\left\{ \begin{array}{l}
4.5 + 3.4 = 32\\
4.\frac{5}{2} + 3.9 = 37\\
4.10 + 3.9 = 67\\
4.10 + 3.2 = 46
\end{array} \right.\)

\( \Rightarrow {F_{\min }} = 32\).