Cho \(x,y\) thoả mãn hệ \(\left\{ \begin{array}{l}x + 2y - 100 \le 0\\2x\,\, + \,y - 80\,\, \le 0\\x \ge 0\\y \ge 0\end{array} \right.\). Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức \(P = \left( {x;y} \right) = 40000x + 30000y\).
-
A.
\({P_{\max }} = 2000000.\)
-
B.
\({P_{\max }} = 2400000.\)
-
C.
\({P_{\max }} = 1800000.\)
-
D.
\({P_{\max }} = 1600000.\)
Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm \(S\) là đa giác.
Bước 2: Tính giá trị của \(F\) tương ứng với \(\left( {x;y} \right)\) là tọa độ của các đỉnh của đa giác.
Bước 3: Kết luận:
\( \bullet \) Giá trị lớn nhất của \(F\) là số lớn nhất trong các giá trị tìm được.
\( \bullet \) Giá trị nhỏ nhất của \(F\) là số nhỏ nhất trong các giá trị tìm được.
Trong mặt phẳng tọa độ \(Oxy\), vẽ các đường thẳng:
\({d_1}:x + 2y - 100 = 0,\,\,{\rm{ }}{d_2}:2x + y - 80 = 0\).
Lấy điểm bất kì \(P(10;10)\).
+) \(x + 2y - 100 = 10 + 20 - 100 = - 70 \le 0\).
+) \(2x + y - 80 = 20 + 10 - 80 = - 50 \le 0\).
Do đó \(P(10;10) \in \) miền nghiệm.
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (tứ giác \(OABC\) kể cả biên) tô màu như hình vẽ.
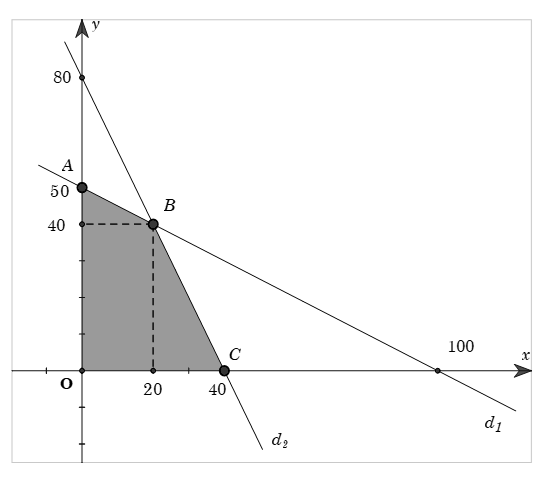
Xét các đỉnh của miền khép kín tạo bởi hệ là
\(\begin{array}{l}O\left( {0;0} \right),\,\,A\,\left( {0;50} \right),\,\,B\left( {20;40} \right),C\left( {40;0} \right).\end{array}\)
Ta có \(\left\{ \begin{array}{l}P\left( {0;0} \right) = 0\\P\left( {0;50} \right) = 1500000\\P\left( {20;40} \right) = 2000000\\P\left( {40;0} \right) = 1600000\end{array} \right.\)
Đáp án : A

Các bài tập cùng chuyên đề
Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là \(1300\) mg. trong 1 lạng đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi.
(Nguồn: https://hongngochospital.vn)
Gọi \(x,y\) lần lượt là số lạng đậu nành và số lạng thịt mà một người đang độ tuổi trưởng thành ăn trong một ngày
a) Viết bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng canxi cần thiết trong một ngày của một người trong độ tuổi trưởng thành.
b) Chỉ ra một nghiệm \(\left( {{x_0};{y_0}} \right)\) với \({x_0},{y_0} \in \mathbb{Z}\) của bất phương trình đó.
Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là 300 ca-lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp 60 ca-lo, 6 đơn vị vitamin A và 30 đơn vị vitamin C.
a) Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.
b) Chỉ ra hai phương án mà bác Ngọc có thể chọn lựa số lượng cốc cho đồ uống thứ nhất và thứ hai nhằm đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.
Một chuỗi nhà hàng ăn nhanh bán đồ ăn từ 10h00 sáng đến 22h00 mỗi ngày. Nhân viên phục vụ của nhà hàng làm việc theo hai ca, mỗi ca 8 tiếng, ca I từ 10h00 đến 18h00 và ca II từ 14h00 đến 22h00.
Tiền lương của nhân viên được tính theo giờ (bảng bên).
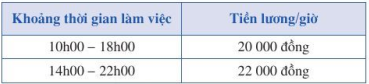
Để mỗi nhà hàng hoạt động được thì cần tối thiểu 6 nhân viên trong khoảng 10h00 - 18h00, tối thiểu 24 nhân viên trong thời gian cao điểm 14h00 - 18h00 và không quá 20 nhân viên trong khoảng 18h00 – 22h00. Do lượng khách trong khoảng 14h00 – 22h00 thường đông hơn nên nhà hàng cần số nhân viên ca II ít nhất phải gấp đôi số nhân viên ca I. Em hãy giúp chủ chuỗi nhà hàng chỉ ra cách huy động số lượng nhân viên cho mỗi ca sao cho chi phí tiền lương mỗi ngày là ít nhất.
Một công ty dự định sản xuất hai loại sản phẩm A và B. Các sản phẩm này được chế tạo từ ba loại nguyên liệu I, II và III. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại nguyên liệu cần dùng để sản xuất ra 1 kg sản phẩm được cho trong bảng sau:
|
Loại nguyên liệu |
Số kilogam nguyên liệu dự trữ |
Số kilogam nguyên liệu cần dùng sản xuất 1 kg sản phẩm |
|
|
A |
B |
||
|
I |
8 |
2 |
1 |
|
II |
24 |
4 |
4 |
|
III |
8 |
1 |
2 |
Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất? Biết rằng, mỗi kilôgam sản phẩm loại A lãi 30 triệu đồng, mỗi kilôgam sản phẩm loại B lãi 50 triệu đồng.
Một công ty cần mua các tủ đựng hồ sơ. Có hai loại tủ: Tủ loại A chiếm 3 \({m^2}\) sàn, loại này có sức chứa 12 \({m^3}\) và có giá 7,5 triệu đồng; tủ loại B chiếm 6 \({m^2}\) sàn, loại này có sức chứa 18 \({m^3}\) và có giá 5 triệu. Cho biết công ty chỉ thu xếp được nhiều nhất là 60 \({m^2}\) mặt bằng cho chỗ đựng hồ sơ và ngân sách mua tủ không quá 60 triệu đồng. Hãy lập kế hoạch mua sắm để công ty có được thể tích đựng hồ sơ lớn nhất.
Một nông trại thu hoạch được 180 kg cà chua và 15 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10 kg cà chua cùng với l kg hành tây và khi bán lãi được 200 nghìn đồng, còn để làm được một hũ tương cà loại B cần 5 kg cà chua cùng với 0,25 kg hành tây và khi bán lãi được 150 nghìn đồng. Thǎm dò thị hiếu của khách hàng cho thấy cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B. Hãy giúp chủ nông trại lập kế hoạch làm tương cà để có được nhiều tiền lãi nhất.
Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày, máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất mỗi ngày sao cho tổng số tiền lãi cao nhất.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(F\left( {x;y} \right) = 2x + 3y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 6}\\{x \ge 0}\\{y \ge 0}\end{array}.} \right.\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(F\left( {x;y} \right) = 4x - 3y\) trên miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \ge - 4}\\{x + y \le 5}\\{x - y \le 5}\\{x - y \ge - 4}\end{array}.} \right.\)
Giá trị lớn nhất của biểu thức \(F\left( {x;y} \right) = 3x + y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{x + y \le 2}\\{y \ge 0}\end{array}} \right.\) là:
A. -3.
B. 6.
C. 5.
D. 8.
Giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x + 4y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 1}\\{x \le 2}\\{y \ge 0}\\{y \le 3}\end{array}} \right.\) là:
A. \( - 2.\)
B. \(3.\)
C. \(11.\)
D. \( - 4.\)
Tổng các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = x + 5y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - 2 \le y \le 2}\\{x + y \le 4}\\{y - x \le 4}\end{array}} \right.\) là:
A. \( - 20.\)
B. \(-4.\)
C. \(28.\)
D. \( 16.\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = 2x + 3y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{y \ge - 1}\\{y \le 1}\\{x + y \le 4}\\{y - x \le 4}\end{array}.} \right.\)
Giá trị nhỏ nhất của biểu thức \(F = - x + y\) trên miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \le 2}\\{ - x + 2y \ge 4}\\{x + y \le 5}\end{array}} \right.\) là:
A. \(0\)
B. 1
C. 2
D. 3
a) Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 5}\\{3x + 2y \le 12}\\{x \ge 1}\\{y \ge 0}\end{array}} \right.\left( {III} \right)\)
b) Tìm x, y là nghiệm của hệ bất phương trình (III) sao cho \(F = 3x + 7y\) đạt giá trị lớn nhất, nhỏ nhất.
Giá trị nhỏ nhất của biểu thức trên miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 2}\\{x + y \le 4}\\{x - 5y \le - 2}\end{array}} \right.\)
A. -5
B. -7
C. 1
D. 4
a) Biểu diễn miền nghiệm của các bất phương trình sau: \(\left\{ {\begin{array}{*{20}{c}}{3x - y \le 9}\\{3x + 6y \le 30}\\{x \ge 0}\\{0 \le y \le 4}\end{array}} \right.\left( I \right)\).
b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x + 4y\) đạt giá trị lớn nhất.
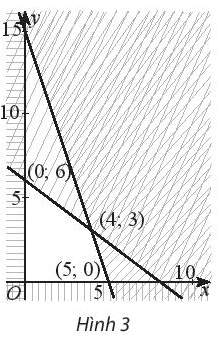
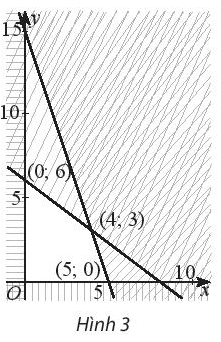
Biểu thức \(F = 2x - 8y\) đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong hình 3?
A. \( - 48\)
B. 0
C. \( - 160\)
D. \( - 40\)
Biểu thức \(F = 5x + 2y\) đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong hình 3?
A. 30
B. 12
C. 25
D. 26
Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây:
|
X |
0 |
0 |
1 |
1 |
2 |
2 |
4 |
|
Y |
2 |
4 |
0 |
1 |
0 |
1 |
0 |
|
\(F= 4x + 5y\) |
|
|
|
|
|
|
|
|
\(G = 5x - 3y\) |
|
|
|
|
|
|
|
Trong các giá trị tìm được:
a) Tìm GTLN của F
b) Tìm GTNN của G
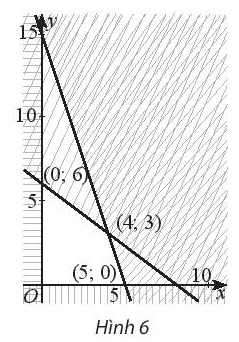
Trên miền đa giác không gạch chéo ở hình 6, hãy:
a) Tìm GTLN của \(F = 2x + 3y\)
b) Tìm GTNN của \(G = x - 4y\)
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + y \le 6\\3x - 4y \le 6\\5x - 2y \ge 0\\x \le 2\\y \ge - 1\end{array} \right.\)
có miền nghiệm là miền ngũ giác ABCDE như hình dưới. Giá trị nhỏ nhất của \(F = 15x - 9y\) là:
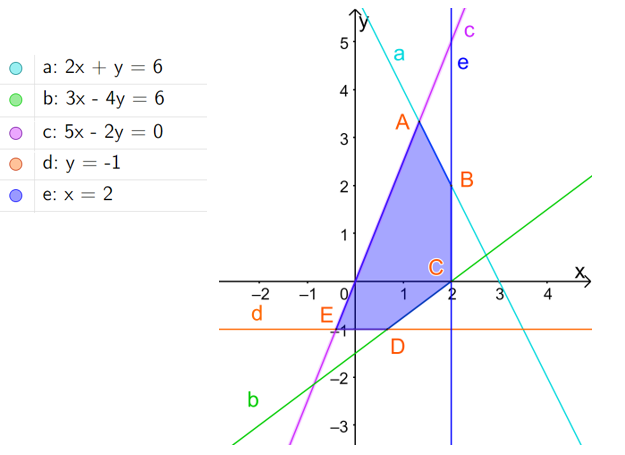
-
A.
\(-30\)
-
B.
\(-10\)
-
C.
\(12\)
-
D.
\(19\)
a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x - 2y \ge - 6\\2x + y \le 10\end{array} \right.\).
b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y) = 2x +3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.
Cho hệ bất phương trình sau: $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ và biểu thức $F = 3x + 5y$. Các mệnh đề sau đúng hay sai?
a) Điểm $B\left( {\dfrac{5}{2};\dfrac{5}{4}} \right)$ là điểm thuộc miền nghiệm của hệ bất phương trình thỏa mãn $F = 3x + 5y$đạt giá trị lớn nhất.
b) Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ là miền tam giác.
c) Miền nghiệm của bất phương trình $5x - y \geq - 4$ là nửa mặt phẳng bờ là $d:5x - y = - 4$và chứa gốc tọa độ O, kể cả bờ.
d) Điểm $M\left( {1;2024} \right)$ thỏa mãn miền nghiệm của hệ bất phương trình.
Cho hệ bất phương trình $\left\{ \begin{array}{l} {2x + 3y - 6 \leq 0} \\ {x \geq 0} \\ {2x - 3y - 1 \leq 0} \end{array} \right.$. Các mệnh đề sau đúng hay sai?
a) Hệ trên là một hệ bất phương trình bậc nhất hai ẩn.
b) (0;0) là một nghiệm của hệ bất phương trình trên.
c) (1;-1) là một nghiệm của hệ bất phương trình trên.
d) Với x, y thỏa mãn hệ bất phương trình đã cho, biểu thức $L = y - x$ đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b và $a + 2b = \dfrac{13}{12}$.







Danh sách bình luận