Đề bài
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\2x + 3y > 6\end{array} \right.\) là phần không gạch trong hình nào dưới đây?
-
A.
-
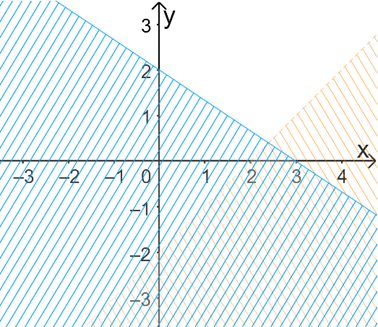
B.
-
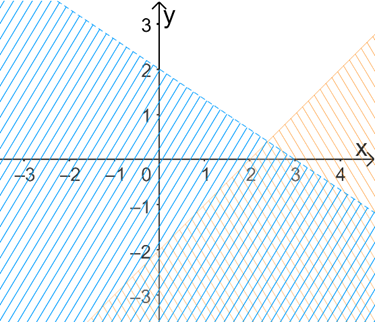
C.
-
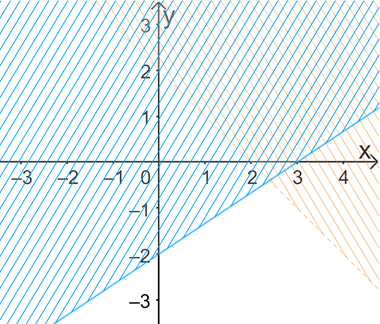
D.
Phương pháp giải
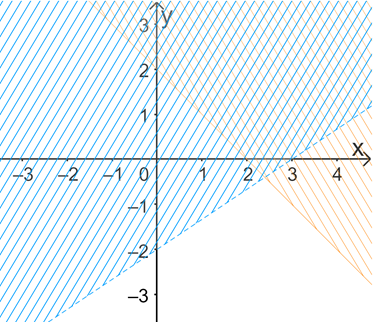
Bước 1: Chỉ ra điểm một điểm thuộc miền nghiệm.
Bước 2: Xác định các bờ là nét đứt hay nét liền.
+) Miền nghiệm của hệ chứa các điểm thuộc đường thẳng d \( \Rightarrow\) Vẽ d nét liền.
+) Ngược lại \( \Rightarrow\) Vẽ d nét đứt.
Lời giải của GV Loigiaihay.com
+ Lấy điểm \(A(0;3)\) không thuộc \(d:x - y = 2\) và \(\Delta :2x + 3y = 6\).
+ Điểm \(A(0;3)\) thuộc miền nghiệm vì \(\left\{ \begin{array}{l}0 - 3 = - 3 \le 2\\2.0 + 3.3 = 9 > 6\end{array} \right.\)
\( \Rightarrow\) Loại C, D.
Miền nghiệm của hệ bất phương trình chứa các điểm thuộc đường thẳng \(d:x - y = 2\).
Vì d nét liền \( \Rightarrow\) Loại A.
Đáp án : B
Danh sách bình luận