Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\) là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông cân
-
C.
Tam giác vuông
-
D.
Tam giác đều.
+) Dựa vào tính chất của các đường cao trong tam giác.
+) Dựa vào tính chất của tam giác cân.
+) Đường trung tuyến ứng với cạnh huyền của tam giác vuông bằng nửa cạnh huyền.
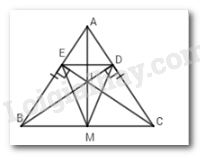
Xét \(\Delta ABC\) có $BD$ và $CE$ là hai đường cao cắt nhau tại $I$ suy ra $AI$ là đường cao của tam giác đó.
Mà $AI$ cắt $BC$ tại $M$ nên \(AM \bot BC\).
Vì \(\Delta ABC\) cân tại $A$ (gt) nên $AM$ là đường cao cũng chính là đường trung tuyến của tam giác đó. (tính chất của tam giác cân).
\( \Rightarrow BM = MC\) (tính chất đường trung tuyến)
Vì \(\left\{ \begin{array}{l}CE \bot AB\\BD \bot AC\end{array} \right. \Rightarrow \widehat {BEC} = \widehat {BDC} = {90^0}\).
Xét \({\Delta}BEC\) có $M$ là trung điểm của $BC$ nên suy ra $EM$ là trung tuyến của \({\Delta}BEC\)
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (tính chất trung tuyến của tam giác vuông)
Xét \({\Delta}BDC\) có $M$ là trung điểm của $BC$ nên $DM$ là trung tuyến của \({\Delta}BDC\)
\( \Rightarrow DM = \dfrac{{BC}}{2}\left( 2 \right)\) (tính chất trung tuyến của tam giác vuông)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow EM = DM \Rightarrow \Delta EMD\) cân tại $M$ (dấu hiệu nhận biết tam giác cân).
Đáp án : A
Các bài tập cùng chuyên đề
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
-
A.
Điểm cách đều ba cạnh của \(\Delta ABC\).
-
B.
Điểm cách đều ba đỉnh của \(\Delta ABC\).
-
C.
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
-
D.
Đáp án B và C đúng
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
-
A.
Tam giác vuông
-
B.
Tam giác cân
-
C.
Tam giác đều
-
D.
Tam giác vuông cân
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({40^0}\).
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
-
A.
\(20^\circ \)
-
B.
\(30^\circ \)
-
C.
\(40^\circ \)
-
D.
\(50^\circ \)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
-
A.
\(\Delta ADE\) là tam giác cân
-
B.
$HA$ là tia phân giác của \(\widehat {MHN}\).
-
C.
A, B đều đúng
-
D.
A, B đều sai
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
-
A.
$BM$ là đường trung tuyến của \(\Delta ABC\)
-
B.
\(BM = AB\).
-
C.
$BM$ là phân giác của \(\widehat {ABC}\).
-
D.
$BM$ là đường trung trực của \(\Delta ABC\).
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
-
A.
\(\Delta AHD = \Delta AKD\)
-
B.
$AD$ là đường trung trực của đoạn thẳng $HK.$
-
C.
\(AD\) là tia phân giác của góc \(HAK.\)
-
D.
Cả A, B, C đều đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
-
A.
\(AM \bot BC\)
-
B.
\(AM\) là đường trung trực của \(BC\)
-
C.
\(AM\) là đường phân giác của góc \(BAC.\)
-
D.
Cả A, B, C đều đúng.
Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.
-
A.
\(AB + AC > HA + HB + HC\)
-
B.
\(AB + AC < HA + HB + HC\)
-
C.
\(AB + AC = HA + HB + HC\)
-
D.
\(AB + AC \le HA + HB + HC\)
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({90^0}\).
