Đề bài
Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\) Chọn câu đúng.
-
A.
\(BH = BD\)
-
B.
\(BH > BA\)
-
C.
\(BH < BA\)
-
D.
\(BH = BA\)
Phương pháp giải
Chứng minh hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau
Lời giải của GV Loigiaihay.com
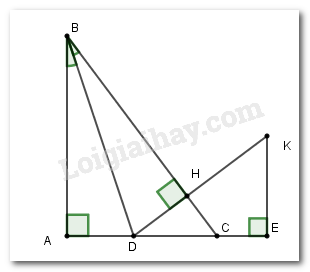
Xét tam giác vuông \(BAD\) và \(BHD\) có
\(AD\) chung
\(\widehat {ABD} = \widehat {HBD}\) (tính chất tia phân giác)
Nên \(\Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Đáp án : D
