Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
-
A.
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
-
B.
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
-
C.
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
-
D.
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
+ Tính số đo góc AOC nhờ bài toán biết tổng và hiệu.
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
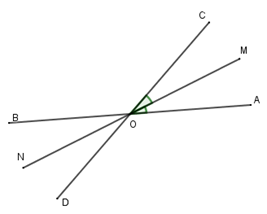
Ta có: \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \) ( 2 góc kề bù)
Mà \(\widehat {AOD} - \widehat {AOC} = 60^\circ \)
suy ra \(\widehat {AOC} = \left( {180^\circ - 60^\circ } \right):2 = 60^\circ \)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \frac{{\widehat {COA}}}{2} = \frac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Đáp án : B

Các bài tập cùng chuyên đề
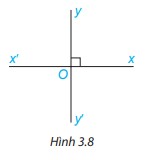
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
Vẽ góc xOy có số đo bằng 60 \(^\circ \). Vẽ tia Om là tia đối của tia Ox.
a) Gọi tên hai góc kề bù có trong hình vừa vẽ.
b) Tính số đo góc yOm.
c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.
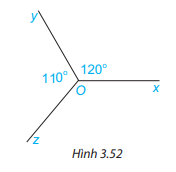
Cho Hình 3.52, biết \(\widehat {xOy} = 120^\circ ,\widehat {yOz} = 110^\circ \). Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia Oy
Tìm số đo các góc còn lại trong mỗi hình sau:
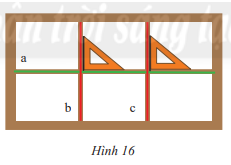
Cặp cạnh nào của các ô cửa sổ (Hình 16) vuông góc với nhau? Hãy dùng kí hiệu (\( \bot \)) để biểu diễn chúng.
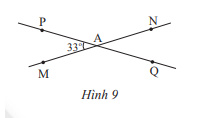
Cho đường thẳng MN, PQ cắt nhau tại A và tạo thành \(\widehat {PAM} = 33^\circ \) (Hình 9)
a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ \). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ \) và \(\widehat {zOt} = 135^\circ \). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 142^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {x'Oz}\)
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 120^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\), Oz’ là tia phân giác của \(\widehat {yOx'}\). Tính \(\widehat {zOy},\widehat {yOz'},\widehat {zOz'}\)
Vẽ góc bẹt \(\widehat {xOy}\). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của \(\widehat {xOz}\). Vẽ tia phân giác Ov của \(\widehat {zOy}\) . Tính \(\widehat {tOv}\)
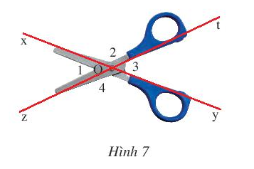
Qua điểm O, là chốt xoay của một cái kéo, kẻ hai đường thẳng xOy và zOt lần lượt song song với hai lưỡi kéo (Hình 7). Tìm các góc kề bù và các góc đối đỉnh có trong hình vẽ.
Trên mặt đồng hồ ở Hình 1, quan sát hai góc: góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.
Hai góc đó có liên hệ gì đặc biệt?
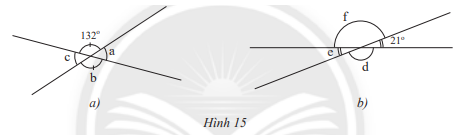
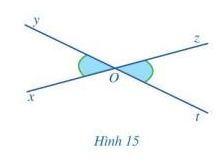
Quan sát Hình 15 và giải thích vì sao:
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\) và \(\widehat {xOy} = \widehat {zOt}\)
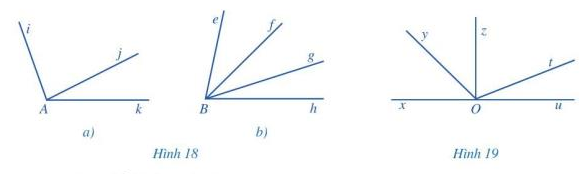
a) Tìm hai góc kề nhau trong mỗi hình 18a, 18b:
b) Tìm hai góc kề bù (khác góc bẹt) ở Hình 19.
c) Tìm hai góc đối đỉnh (khác góc bẹt và góc không) trong mỗi hình 20a, 20b, 20c, 20d:

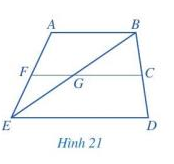
Quan sát Hình 21 và chỉ ra:
a) Hai góc kề nhau;
b) Hai góc kề bù (khác góc bẹt) ;
c) Hai góc đối đỉnh( khác góc bẹt và góc không).
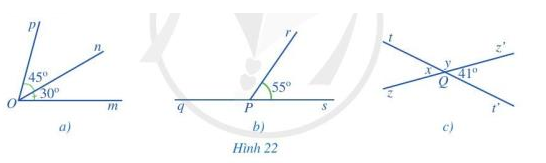
Tìm số đo:
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x,y trong Hình 22c.
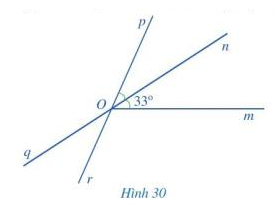
Trong Hình 30, tính số đo của \(\widehat {mOp};\widehat {qOr};\widehat {pOq}\)
Hai tia phân giác của hai góc đối đỉnh là
-
A.
Hai tia trùng nhau
-
B.
Hai tia vuông góc
-
C.
Hai tia đối nhau
-
D.
Hai tia song song
Cho tia Ob nằm giữa hai tia Oa và Oc; \(\widehat{aOb} = \widehat{bOc} = 20^\circ\). Khẳng định nào sau đây sai?
-
A.
\(\widehat{aOc} = 40^\circ\)
-
B.
Ob là tia phân giác của \(\widehat{aOc}\)
-
C.
\(\widehat{aOb}\) và \(\widehat{bOc}\) là hai góc kề nhau
-
D.
Oc là tia phân giác của \(\widehat{aOb}\).
Cho hình 3.5
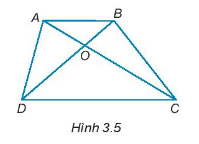
a) Gọi tên các cặp góc đối đỉnh.
b) Gọi tên góc kề bù với \(\widehat {AOD}\)
Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat {xOm} = {120^\circ}\). Tính các góc mOy, yOn, xOn.
Vẽ \(\widehat {xAm} = {50^\circ }\). Vẽ tia phân giác An của \(\widehat {xAm}\).
a) Tính \(\widehat {xAn}\).
b) Vẽ tia Ay là tia đối của tia An. Tính \(\widehat {mAy}\).
Vẽ góc xOy có số đo \({60^o}\). Vẽ tia Om là tia đối của tia Ox.
a) Viết tên hai góc kề bù có trong hình vừa vẽ.
b)Tìm số đo góc yOm
c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.
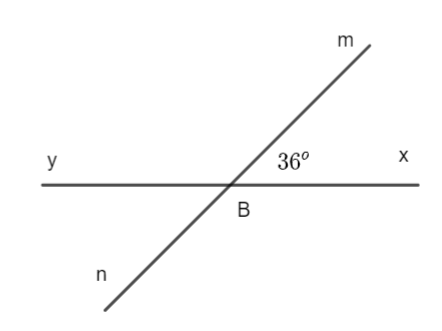
Cho hình 3.4 biết \(\widehat {xBm} = {36^o}\). Tính số đo các góc còn lại trong hình vẽ.
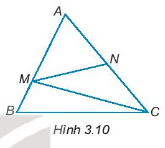
Cho hình 3.10
a) Viết tên góc so le trong với góc NMC
b) Viết tên góc đồng vị với góc ACB, góc AMN.
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là \({65^0}\). Khi đó số đo của ba góc còn lại là:
A. \({65^0};{115^0};{120^0};\)
B. \({65^0};{65^0};{115^0};\)
C. \({115^0};{115^0};{50^0};\)
D. \({65^0};{115^0};{115^0}.\)
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
A.\({70^0};{70^0};{70^0};{110^0}\)
B. \({60^0};{120^0};{120^0};{120^0};\)
C. \({80^0};{50^0};{130^0};{100^0};\)
D. \({90^0};{90^0};{90^0};{90^0}.\)
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = {30^0}\). Số đo của góc AOC bằng:
A.\({30^0};\)
B. \({60^0};\)
C. \({120^0};\)
D. Một kết quả khác.
Cho hình 3.29.
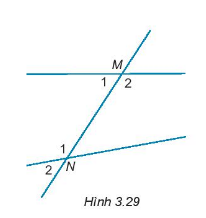
a) Cặp góc so le trong là cặp góc
A.\(\widehat {{M_1}},\widehat {{M_2}};\)
B. \(\widehat {{M_1}},\widehat {{N_1}};\)
C. \(\widehat {{M_1}},\widehat {{N_2}};\)
D. \(\widehat {{M_2}},\widehat {{N_1}}.\)
b) Cặp góc đồng vị là cặp góc:
A.\(\widehat {{M_1}},\widehat {{M_2}};\)
B. \(\widehat {{M_1}},\widehat {{N_1}};\)
C. \(\widehat {{M_1}},\widehat {{N_2}};\)
D. \(\widehat {{M_2}},\widehat {{N_1}}.\)
Cho hình 3.35. Biết CN là tia phân giác của góc ACM.
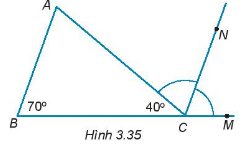
a) Chứng minh rằng \(CN//AB\).
b) Tính số đo của góc A.








Danh sách bình luận