Tính A = 1 + 3 + 32 +…+ 32022
-
A.
\(\frac{{{3^{2023}} + 1}}{2}\)
-
B.
\({3^{2023}}\)
-
C.
\({3^{2023}} - 1\)
-
D.
\(\frac{{{3^{2023}} - 1}}{2}\)
Phát hiện quy luật của tổng
Bước 1: Tìm 3.A
Bước 2: Thực hiện tính 3A – A
Bước 3: Tính A
Ta có: A = 1 + 3 + 32 +…+ 32022
suy ra 3.A = 3. ( 1 + 3 + 32 +…+ 32022) = 3 + 32 + 33 +…+ 32023
do đó 3. A – A = 3 + 32 + 33 +…+ 32023 – (1 + 3 + 32 +…+ 32022)
2A = 3 + 32 + 33 +…+ 32023 – 1 - 3 - 32 - …- 32022 = 32023 – 1
suy ra \( A = \frac{{{3^{2023}} - 1}}{2}\)
Đáp án : D

Các bài tập cùng chuyên đề
Bảng thống kê dưới đây cho biết lượng khách quốc tế đến thăm Việt Nam trong năm 2019.
|
Quốc gia |
Số khách đến thăm |
|
Hàn Quốc |
\(4,{3.10^6}\) |
|
Hoa Kì |
\(7,{4.10^5}\) |
|
Pháp |
\(2,{9.10^5}\) |
|
Ý |
\({7.10^4}\) |
Em hãy sắp xếp tên các quốc gia theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn.
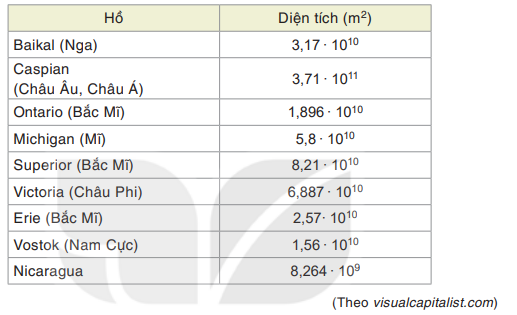
Diện tích mặt nước của một số hồ nước ngọt lớn nhất trên thế giới được cho trong bảng sau. Em hãy sắp xếp chúng theo thứ tự diện tích từ nhỏ đến lớn.
Tính giá trị của các biểu thức sau:
\(\begin{array}{l}a)\frac{{{3^{12}} + {3^{15}}}}{{1 + {3^3}}}\\b)2:{\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 0,{125^3}{.8^3} - {( - 12)^4}:{6^4}\end{array}\)
Tính:
a) \({\left( {1 + \frac{1}{2} - \frac{1}{4}} \right)^2}.\left( {2 + \frac{3}{7}} \right)\)
b) \(4:{\left( {\frac{1}{2} - \frac{1}{3}} \right)^3}\)
Tính nhanh.
\(M = \left( {100 - 1} \right).\left( {100 - {2^2}} \right).\left( {100 - {3^2}} \right)...\left( {100 - {{50}^2}} \right)\)
Tính giá trị các biểu thức.
a)\(\frac{{{4^3}{{.9}^7}}}{{{{27}^5}{{.8}^2}}};\)
b)\(\frac{{{{\left( { - 2} \right)}^3}.{{\left( { - 2} \right)}^7}}}{{{{3.4}^6}}};\)
c)\(\frac{{{{\left( {0,2} \right)}^5}.{{\left( {0,09} \right)}^3}}}{{{{\left( {0,2} \right)}^7}.{{\left( {0,3} \right)}^4}}};\)
d)\(\frac{{{2^3} + {2^4} + {2^5}}}{{{7^2}}}.\)
Tính:
a)\({\left( {\frac{2}{5} + \frac{1}{2}} \right)^2}\); b)\({\left( {0,75 - 1\frac{1}{2}} \right)^3};\)
c)\({\left( {\frac{3}{5}} \right)^{15}}:{\left( {0,36} \right)^5}\); d)\({\left( {1 - \frac{1}{3}} \right)^8}:{\left( {\frac{4}{9}} \right)^3}\)
Thực hiện phép tính.
a) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)
b)\({\left( { - 0,2} \right)^2}.5 - \frac{{{2^{13}}{{.27}^3}}}{{{4^6}{{.9}^5}}};\)
c)\(\frac{{{5^6} + {2^2}{{.25}^3} + {2^3}{{.125}^2}}}{{{{26.5}^6}}}.\)
Biết vận tốc ánh sáng xấp xỉ bằng \(299\,792\,458\;{\rm{m/s}}\) và ánh sáng Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất. (Nguồn: https://vi.wikipedia.org)
Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
Chu kì bán rã của nguyên tố phóng xạ Urani 238 là 4,468 . 109 năm (nghĩa là sau 4,468 . 109 năm khối lượng của nguyên tố đó chỉ còn lại một nửa).
(Nguồn: https://vi.wikipedia.org)
a) Ba chu kì bán rã của nguyên tố phóng xạ đó là bao nhiêu năm?
b) Sau ba chu kì bán rã, khối lượng của nguyên tố phóng xạ đó còn lại bằng bao nhiêu phần khối lượng ban đầu?
Người ta thường dùng các luỹ thừa của 10 với số mũ nguyên dương để biểu thị những số rất lớn. Ta gọi một số hữu tỉ dương được viết theo kí hiệu khoa học (hay theo dạng chuẩn) nếu nó có dạng a.10n với \(1 \le a < 10\) và n là một số nguyên dương. Ví dụ, khối lượng của Trái Đất viết theo kí hiệu khoa học là 5,9724.1024 kg.
Viết các số sau theo kí hiệu khoa học (với đơn vị đã cho):
a) Khoảng cách giữa Mặt Trăng và Trái Đất khoảng 384 400 km;
b) Khối lượng của Mặt Trời khoảng 1989 . 1027 kg;
c) Khối lượng của Sao Mộc khoảng 1 898 . 1024 kg.
(Nguồn: https://www.nasa.gov)
Sử dụng máy tính cầm tay
Nút luỹ thừa: (ở một số máy tính nút luỹ thừa còn có dạng
![]() )
)
Nút phân số:![]()
Nút chuyển xuống để ghi số hoặc dấu:![]()
Nút chuyển sang phải để ghi số hoăc dấu:![]()
Dùng máy tính cầm tay để tính:
a) \({(3,147)^3};\)
b) \({( - 23,457)^5};\)
c) \({\left( {\frac{4}{{ - 5}}} \right)^4}\);
d) \({(0,12)^2} \cdot {\left( {\frac{{ - 13}}{{28}}} \right)^5}\).
Tính:
a) \(5\frac{3}{4}.\frac{{ - 8}}{9}\)
b) \(3\frac{3}{4}:2\frac{1}{2}\)
c) \(\frac{{ - 9}}{5}:1,2\)
d) \({\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}}\).
Tìm số tự nhiên n, biết:
a) \({5^n}.{\left( {\dfrac{1}{5}} \right)^3} = 125\)
b) \(4.3^n = 324\)
Tính: \(A = \dfrac{{{{27}^{10}} + {9^5}}}{{{9^{13}} + {{27}^2}}}\)
Tính
a) \({\left( {\dfrac{2}{5} - \dfrac{1}{3}} \right)^2}\)
b) \({\left( {1\dfrac{1}{2} - 1,25} \right)^3}\)
c) \({\left( {\dfrac{1}{2} + \dfrac{1}{3}} \right)^2}:{\left( {1\dfrac{1}{2}} \right)^2}\)
d) \(2:{\left( {\dfrac{1}{2} - \dfrac{2}{3}} \right)^3}\)
Tính giá trị các biểu thức
a) \(\dfrac{{{9^3}{{.2}^{10}}}}{{{{16}^2}{{.81}^2}}}\)
b) \(\dfrac{{{{( - 3)}^7}.{{( - 3)}^8}}}{{{{7.9}^7}}}\)
c) \(\dfrac{{{{(0,3)}^6}.{{(0,04)}^3}}}{{{{(0,09)}^4}.{{(0,2)}^4}}}\)
d) \(\dfrac{{{2^3} + {2^4} + {2^5} + {2^6}}}{{{{15}^2}}}\)
Khối lượng một số hành tinh trong Hệ Mặt Trời:
Sao Thổ 5,6846 . 1026 kg, Sao Mộc 1,8986 . 1027 kg, Sao Thiên Vương 8,6810 . 1025 kg, Sao Hải Vương 10,243 . 1025 kg, Trái Đất 5,9736 . 1024 kg.
a) Sắp xếp khối lượng các hành tinh trên theo thứ tự từ nhẹ đến nặng.
b) Trong các hành tinh trên, hành tinh nào nhẹ nhất, hành tinh nào nặng nhất?
Chọn từ “bằng nhau”, “đối nhau” thích hợp cho ?:
a) Nếu hai số đối nhau thì bình phương của chúng ?;
b) Nếu hai số đối nhau thì lập phương của chúng ?;
c) Lũy thừa chẵn cùng bậc của hai số đối nhau thì ?;
d) Lũy thừa lẻ cùng bậc của hai số đối nhau thì ?.
Bạn Na viết một trang web để kết bạn. Trang web đã nhận được 3 lượt truy cập trong tuần đầu tiên. Nếu số lượt truy cập tuần tiếp theo gấp 3 lần số lượt truy cập tuần trước thì sau 6 tuần đầu tiên, trang web của bạn Na có tất cả bao nhiêu lượt truy cập?
a) Rút gọn biểu thức: \(A = 1 + 2 + {2^1} + {2^2} + ... + {2^{25}}\).
b) Một công ty phát triển kĩ thuật số có một thông báo hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 26 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
- Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 50 triệu đồng.
- Phương án 2: Ngày đầu nhận 1 đồng, ngày sau nhận gấp đôi ngày trước đó.
Theo em, phương án nào nhận được nhiều tiền công hơn? Vì sao?
Tính:
a, \({\left( {1 + \frac{1}{2} - \frac{1}{4}} \right)^2}.\left( {2 + \frac{3}{7}} \right);\)
b, \(4:{\left( {\frac{1}{2} - \frac{1}{3}} \right)^3}.\)
Tính \(A = \left( {{{\left( {\frac{1}{{125}}} \right)}^3} + {{\left( {\frac{1}{5}} \right)}^5}} \right):\left( {{{\left( {\frac{1}{5}} \right)}^5} + \frac{1}{5}} \right).\)
Bảng dưới đây cho ta kích thước đường kính của một số hành tinh (tính theo dặm, dặm là đơn vị đo độ dài của nước Anh và Mỹ, 1 dặm =1609,344 m)

Em hãy sắp xếp các hành tinh trên theo thứ tự đường kính từ nhỏ đến lớn.
-
A.
5 lần;
-
B.
5 . 108 lần;
-
C.
8 lần;
-
D.
108 lần.
Biểu thức (27)5 : (− 32)3 được viết dưới dạng lũy thừa của một số hữu tỉ là
-
A.
\({\left( { - \frac{3}{2}} \right)^{15}}\);
-
B.
\({\left( { - \frac{{27}}{{32}}} \right)^2}\);
-
C.
\({\left( {\frac{3}{2}} \right)^{15}}\);
-
D.
\({\left( {\frac{{27}}{{32}}} \right)^2}\).
Viết biểu thức 68.125 dưới dạng 2a.3b thì giá trị của a + b là:
-
A.
13
-
B.
31
-
C.
25
-
D.
19
Biết \({1^2} + {2^2} + {3^2} + ... + {8^2} + {9^2} = 285\)
Tính một cách hợp lí giá trị của biểu thức:
\({2^2} + {4^2} + {6^2} + ... + {16^2} + {18^2}\)
Thực hiện phép tính
\(a)\dfrac{{{5^4}{{.20}^4}}}{{{{25}^5}{{.4}^5}}}\)
\(b)\dfrac{{{4^3}{{.25}^5}{{.9}^3}}}{{{8^2}{{.125}^3}{{.3}^5}}}\)
\(c)\dfrac{{{6^3} + {{3.6}^2} + {3^3}}}{{ - 13}}\)
Tính \(B = \frac{{{8^5} + {4^6}}}{{{2^{15}} + {{64}^3}}}.\)







Danh sách bình luận