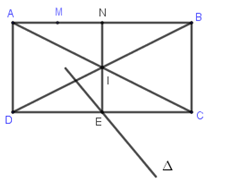
Trong mặt phẳng với hệ tọa độ $Oxy,$  cho hình chữ nhật $ABCD$  có điểm $I\left( {6;2} \right)$ là giao điểm của $2$  đường chéo $AC$  và $BD.$  Điểm $M\left( {1;5} \right)$ thuộc đường thẳng $AB$  và trung điểm $E$  của cạnh $CD$  thuộc đường thẳng $\Delta :x + y-5 = 0.$  Viết phương trình đường thẳng $AB.$

Cho đường thẳng ${d_1}:x + 2y - 7 = 0$ và ${d_2}:2x - 4y + 9 = 0$. Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.

Tính góc tạo bởi giữa hai đường thẳng \({d_1}:6x - 5y + 15 = 0\) và ${d_2}:\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right..$

Cho hai đường thẳng ${d_1}:3x + 4y + 12 = 0$ và ${d_2}:\left\{ \begin{array}{l}x = 2 + at\\y = 1 - 2t\end{array} \right.$. Tìm các giá trị của tham số \(a\) để \({d_1}\) và \({d_2}\) hợp với nhau một góc bằng \({45^0}.\)

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho điểm \(M\left( {{x_0};{y_0}} \right)\) và đường thẳng $\Delta :ax + by + c = 0$. Khoảng cách từ điểm \(M\) đến \(\Delta \) được tính bằng công thức:

Khoảng cách từ giao điểm của hai đường thẳng \(x - 3y + 4 = 0\) và \(2x + 3y - 1 = 0\) đến đường thẳng $\Delta :3x + y + 4 = 0$ bằng:

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có $A\left( {1;2} \right),$ $B\left( {0;3} \right)$ và $C\left( {4;0} \right)$. Chiều cao của tam giác kẻ từ đỉnh \(A\) bằng:

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có $A\left( {3; - 4} \right),$ $B\left( {1;5} \right)$ và $C\left( {3;1} \right)$. Tính diện tích tam giác \(ABC\).

Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \).

Cho đường thẳng $\left( \Delta  \right):3x - 2y + 1 = 0$ . Viết PTĐT $\left( d \right)$  đi qua điểm $M\left( {1;2} \right)$  và  tạo với $\left( \Delta  \right)$  một góc ${45^0}$

Lập phương trình đường thẳng \(\Delta\) đi qua M(2;7) và cách N(1;2) một khoảng bằng 1.

Cho đường thẳng \(d\) có ptts: \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 + t\end{array} \right.;t \in R\). Tìm điểm \(M \in d\) sao cho khoảng cách từ $M$ đến điểm \(A(0;1)\) một khoảng bằng $5.$

Cho \(d:x + 3y - 6 = 0;d':3x + y + 2 = 0.\)   Lập phương trình hai đường phân giác của các góc tạo bởi $d$  và $d'$

Lập phương trình đường phân giác trong của góc $A$  của \(\Delta ABC\) biết \(A\left( {2;0} \right);B\left( {4;1} \right);C\left( {1;2} \right)\)

Trong mặt phẳng với hệ toạ độ $Oxy,$  cho hình vuông $ABCD$  biết  $M\left( {2;1} \right);N\left( {4;-2} \right);P\left( {2;0} \right);Q\left( {1;2} \right)$  lần lượt thuộc cạnh $AB,BC,CD,AD.$  Hãy lập phương trình  cạnh $AB$  của hình vuông.

Trong mặt phẳng với hệ toạ độ $Oxy$, cho $2$ đường thẳng ${d_1}:x - 7y + 17 = 0,$

 ${d_2}:x + y - 5 = 0.$ Viết phương trình đường thẳng $d$ qua điểm $M\left( {0;1} \right)$ tạo với ${d_1},{d_2}$ một tam giác cân tại giao điểm của ${d_1},{d_2}$.

Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$  Đỉnh $A$  có tọa độ là các số dương, hai điểm $B$  và $C$  nằm trên trục $Ox,$  phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$  tìm tọa độ các đỉnh $A,B,C.$

Trong mặt phẳng với hệ toạ độ $Oxy,$  cho $4$ điểm $A\left( {1;0} \right),B\left( {-2;4} \right),C\left( {-1;4} \right),D\left( {3;5} \right).$ Tìm toạ độ điểm $M$  thuộc đường thẳng $(\Delta ):3x - y - 5 = 0$ sao cho hai tam giác $MAB,MCD$  có diện tích bằng nhau.

Trong mặt phẳng với hệ toạ độ $Oxy,$ cho \(\Delta ABC\) có đỉnh $A\left( {1;2} \right),$ phương trình đường trung tuyến \(BM:2x + y + 1 = 0\) và phân giác trong \(CD:x + y - 1 = 0\). Viết phương trình đường thẳng $BC.$

Trong mặt phẳng với hệ toạ độ $Oxy,$  cho tam giác $ABC$  có phương trình đường phân giác trong góc $A$  là ${d_1}:x + y + 2 = 0,$  phương trình đường cao vẽ từ $B$  là ${d_2}:2x-y + 1 = 0,$   cạnh $AB$  đi qua $M\left( {1;-1} \right).$  Tìm phương trình cạnh $AC.$

Xét trong mặt phẳng tọa độ \(Oxy\), cặp điểm nào dưới đây nằm cùng phía so với đường thẳng \(x - 2y + 3 = 0\)?