Trong mặt phẳng với hệ toạ độ $Oxy,$ cho \(\Delta ABC\) có đỉnh $A\left( {1;2} \right),$ phương trình đường trung tuyến \(BM:2x + y + 1 = 0\) và phân giác trong \(CD:x + y - 1 = 0\). Viết phương trình đường thẳng $BC.$
-
A.
$4x + 3y + 4 = 0$
-
B.
$4x - 5y + 4 = 0$
-
C.
$4x + 6y + 4 = 0$
-
D.
$4x + 3y - 4 = 0$
- Gọi tọa độ điểm \(C\) theo phương trình của \(CD\) và tìm tọa độ \(C\) với chú ý điểm \(M \in BM\) mà \(M\) là trung điểm \(AC\)
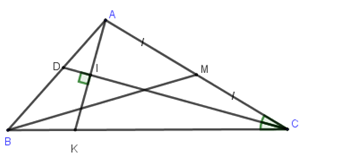
- Kẻ \(AI \bot CD\left( {I \in CD} \right)\) cắt \(BC\) tại \(K\)
- Viết phương trình \(AI\) suy ra tọa độ của \(I = AI \cap CD\)
- Tìm tọa độ của \(K\) với chú ý \(I\) là trung điểm của \(AK\)
- Viết phương trình \(CK\) chính là \(BC\) và kết luận.
Điểm \(C \in CD:x + y - 1 = 0 \Rightarrow C\left( {t;1 - t} \right)\).
Suy ra trung điểm $M$ của $AC$ là \(M\left( {\dfrac{{t + 1}}{2};\dfrac{{3 - t}}{2}} \right)\).
$M$ thuộc $BM$ nên \((t + 1) + \dfrac{{3 - t}}{2} + 1 = 0 \Rightarrow t = - 7 \Rightarrow C\left( { - 7;8} \right)\)
Từ $A\left( {1;2} \right),$ kẻ \(AI \bot CD\left( {I \in CD} \right)\) cắt \(BC\) tại \(K\)
Suy ra \(AK:\left( {x - 1} \right) - \left( {y - 2} \right) = 0 \Leftrightarrow x - y + 1 = 0\)
Tọa độ điểm $I$ thỏa hệ: \(\left\{ \begin{array}{l}x + y - 1 = 0\\x - y + 1 = 0\end{array} \right. \Rightarrow I\left( {0;1} \right)\)
Tam giác $ACK$ cân tại $C$ nên $I$ là trung điểm của $AK \Rightarrow K\left( { - 1;0} \right)$
Đường thẳng $BC$ đi qua $C,K$ nên có phương trình:
\(\dfrac{{x + 1}}{{ - 7 + 1}} = \dfrac{y}{8} \Leftrightarrow 4x + 3y + 4 = 0\)
Đáp án : A








Danh sách bình luận