Sử dụng một nguồn điện xoay chiều có biểu thức điện áp là: \(u\left( t \right)={{U}_{0}}\text{.cos 100}\pi t\left( V \right)\), cấp cho một đoạn mạch điện gồm điện trở, tụ điện và cuộn cảm thuần mắc nối tiếp như hình vẽ:

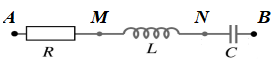
Điện áp hiệu dụng đo được như sau:

Ta có:

\(\left\{ {\begin{array}{*{20}{l}}{{U_{AM}} = {U_R}}\\{{U_{MN}} = {U_L}}\\{{U_{NB}} = {U_C} = 100V}\end{array}} \right.\)

+ Điện áp hai đầu AB:

\(U_{AB}^{2}=U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}\)

\(\Leftrightarrow U_{R}^{2}+{{\left( {{U}_{L}}-100 \right)}^{2}}={{100}^{2}}\,\,\left( 1 \right)\)

+ Điện áp hai đầu AN:

\(U_{AN}^{2}=U_{R}^{2}+U_{L}^{2}\Leftrightarrow U_{R}^{2}+U_{L}^{2}={{100}^{2}}\,\,\left( 2 \right)\)

+ Lấy \(\left( 1 \right)-\left( 2 \right)\) ta được:

\(U_{L}^{2}-200{{U}_{L}}+{{100}^{2}}-U_{L}^{2}=0\Rightarrow {{U}_{L}}=50V\)

Thay vào (2) ta được:

\(U_{R}^{2}+{{50}^{2}}={{100}^{2}}\Rightarrow {{U}_{R}}=50\sqrt{3}V\)

Hệ số công suất của đoạn mạch:

\(\cos \varphi =\dfrac{{{U}_{R}}}{{{U}_{AB}}}=\dfrac{50\sqrt{3}}{100}=\dfrac{\sqrt{3}}{2}\)

Điện áp hiệu dụng hai đầu đoạn mạch: \(U=100V\)

\(\Rightarrow \) Điện áp cực đại: \({{U}_{0}}=U\sqrt{2}=100\sqrt{2}V\)

Ta có:

\(\left\{ \begin{array}{l}

{U_{AM}} = {U_R}\\

{U_{MN}} = {U_L}\\

{U_{NB}} = {U_C}

\end{array} \right.\)

Có \({{U}^{2}}=U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}\)

\(\Rightarrow U_{AB}^{2}=U_{AM}^{2}+{{\left( {{U}_{MN}}-{{U}_{NB}} \right)}^{2}}\)