Đề bài
Tam giác vuông cân tại $A$ có $AB = 2a$. Đường trung tuyến $BM$ có độ dài là:
-
A.
\(3a\)
-
B.
\(2a\sqrt 2 \)
-
C.
\(2a\sqrt 3 \)
-
D.
\(a\sqrt 5 \)
Phương pháp giải
+ Sử dụng tính chất tam giác cân có $AB = AC = 2a$ .
+ Sử dụng định lý Pitago \(B{C^2} = A{B^2} + A{C^2}\) để tính $BC$ .
+ Sử dụng công thức trung tuyến \(MB_{}^2 = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4}\)
Lời giải của GV Loigiaihay.com
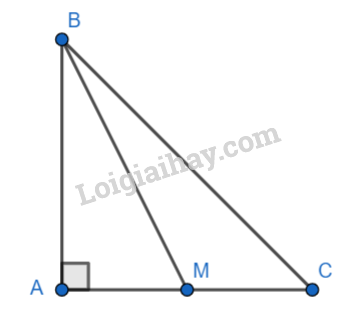
+ Ta có $AB = AC = 2a$ .
+ Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {4{a^2} + 4{a^2}} = 2\sqrt 2 a\)
+ \(MB_{}^2 = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{8{a^2} + 4{a^2}}}{2} - \dfrac{{4{a^2}}}{4} = 5{a^2} \Rightarrow MB = a\sqrt 5 \)
Đáp án : D
Chú ý
Có thể tính \(MB\) bằng định lý pi-ta-go trong tam giác vuông \(AMB\)
