Cho \(M\left( {2;0} \right),\,N\left( {2;2} \right),\,P\left( { - 1;3} \right)\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\) của \(\Delta ABC\). Tọa độ \(B\) là:
-
A.
\(\left( {1;1} \right)\).
-
B.
\(\left( { - 1; - 1} \right)\).
-
C.
\(\left( { - 1;1} \right)\).
-
D.
\(\left( {1; - 1} \right)\).
- Sử dụng tính chất của hình bình hành \(BPNM\) để tìm tọa độ \(B\).
- $BPNM$ là hình bình hành nên $\left\{ \begin{array}{l}{x_B} + {x_N} = {x_P} + {x_M}\\{y_B} + {y_N} = {y_P} + {y_M}\end{array} \right.$
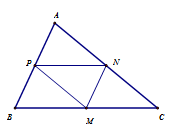
Ta có: $BPNM$ là hình bình hành nên $\left\{ \begin{array}{l}{x_B} + {x_N} = {x_P} + {x_M}\\{y_B} + {y_N} = {y_P} + {y_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + 2 = 2 + ( - 1)\\{y_B} + 2 = 0 + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = - 1\\{y_B} = 1\end{array} \right.$.
Đáp án : C
Các em cũng có thể nhận xét \(BPNM\) là hình bình hành nên \(\overrightarrow {BP} = \overrightarrow {MN} \) và từ đó tính tọa độ của \(B\)







