Cho lục giác đều $ABCDEF$ và \(O\) là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
-
A.
$\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OE} = \overrightarrow 0 $.
-
B.
$\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AD} $.
-
C.
$\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {EB} $.
-
D.
$\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FE} = \overrightarrow 0 $.
- Dựng hình lục giác đều, sử dụng tính chất hình lục giác đều, các véc tơ bằng nhau, đối nhau và quy tắc ba điểm (mở rộng) để kiểm tra tính đúng sai cho từng đáp án.
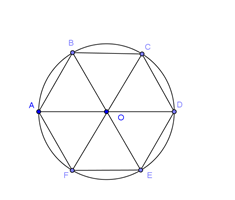
$\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FE} = \overrightarrow {AB} + \overrightarrow {BO} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} \ne \overrightarrow 0 $.
Đáp án : D
Các bài tập cùng chuyên đề
Cho các điểm phân biệt \(A,B,C\). Đẳng thức nào sau đây đúng ?
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
Chọn khẳng định đúng:
Chọn khẳng định sai
Cho hình bình hành \(ABCD\) tâm \(O\). Khi đó \(\overrightarrow {OA} + \overrightarrow {BO} = \)
Cho tam giác đều $ABC$ cạnh $a$. Khi đó $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| bằng $
Cho hình chữ nhật $ABCD$ biết $AB = 4a$ và $AD = 3a$ thì độ dài \(\overrightarrow {AB} + \overrightarrow {AD} \) là:
Cho 6 điểm $A,B,C,D,E,F$. Đẳng thức nào sau đây đúng.
Gọi \(G\) là trọng tâm tam giác vuông$ABC$với cạnh huyền $BC = 12$. Tổng hai vectơ $\overrightarrow {GB} + \overrightarrow {GC} $ có độ dài bằng bao nhiêu ?
Cho hình thoi $ABCD$ tâm $O$, cạnh bằng \(a\) và góc \(A\) bằng \({60^0}\). Kết luận nào sau đây đúng:
Cho tam giác $ABC$. Gọi $M,N,P$ lần lượt là trung điểm các cạnh $AB,AC,BC$. Hỏi $\overrightarrow {MP} + \overrightarrow {NP} $ bằng vec tơ nào?
Cho hình vuông $ABCD$ cạnh $a$, tâm $O$. Khi đó: $\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = $
Cho \(\Delta ABC\) vuông tại \(A\) và \(AB = 3\), \(AC = 4\). Véctơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài bằng
Cho tam giác \(ABC\). Để điểm \(M\) thoả mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \) thì \(M\) phải thỏa mãn mệnh đề nào?
Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :
Cho tam giác đều\(ABC\) cạnh \(a\), trọng tâm là \(G\). Phát biểu nào là đúng?
Cho hình vuông \(ABCD\) có cạnh bằng \(a\). Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng:
Cho tam giác $ABC$. Tập hợp những điểm \(M\) sao cho: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MB} } \right|\) là:
