Một con lắc đơn gồm vật nặng khối lượng \(1kg\), dây treo mảnh, nhẹ , không dãn có chiều dài \(1m\),  kéo con lắc lệch so với phương thẳng đứng góc \(\alpha  = {60^0}\) rồi thả nhẹ. Bỏ qua lực cản không khí, lấy \(10m/{s^2}\). Tìm vận tốc của con lắc khi nó đi qua vị trí  dây treo hợp với phương  thẳng đứng  một góc \({30^0}\).

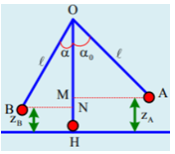
Gọi vị trí vật khi dây treo có phương thẳng đứng là H (Chọn H làm gốc thế năng)

Ta có:

\(\left\{ \begin{array}{l}{z_A} = OH - OM = l - l.\cos {60^0} = l.\left( {1 - \cos {{60}^0}} \right) = 0,5m\\{z_B} = OH - ON = l - l.\cos {30^0} = l.\left( {1 - \cos {{30}^0}} \right) = \dfrac{{2 - \sqrt 3 }}{2}\end{array} \right.\)

Cơ năng tại A:  

Cơ năng tại B: \({W_B} = {W_{tB}} = mg{z_B} + \dfrac{1}{2}mv_B^2\)

Áp dụng định luật bảo toàn cơ năng ta có:

\(\begin{array}{l}{W_A} = {W_B} \Leftrightarrow mg{z_A} = mg{z_B} + \dfrac{1}{2}mv_B^2\\ \Rightarrow {v_B} = \sqrt {2g.\left( {{z_A} - {z_B}} \right)}  = \sqrt {2.10.\left( {0,5 - \dfrac{{2 - \sqrt 3 }}{2}} \right)} \\ \Rightarrow {v_B} = \sqrt {10\sqrt 3  - 10} \,\left( {m/s} \right)\end{array}\)