Trên đường tròn lượng giác với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác \(AM\) có số đo \({75^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua gốc tọa độ \(O\), số đo cung lượng giác \(AN\) bằng:
-
A.
\({255^0}\).
-
B.
\( - \,\,{105^0}\).
-
C.
\( - \,\,{105^0}\) hoặc \({255^0}\).
-
D.
\( - \,\,{105^0} + k{360^0},\,\,k \in \mathbb{Z}\).
Xác định vị trí các điểm \(M,N\) và suy ra số đo cung lượng giác \(AN\).
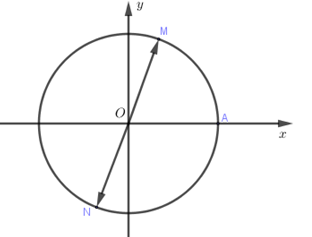
Ta có \(\widehat {AOM} = {75^0}\), \(\widehat {MON} = {180^0} \Rightarrow \widehat {AON} = {105^0}\)
Do đó, cung lượng giác \(AN\) có số đo bằng \( - {105^0} + k{360^0},\,\,\,k \in \mathbb{Z}\).
Đáp án : D
Cũng có thể lý luận như sau: số đo cung \(AN = {255^0} + k{360^0},k \in \mathbb{Z}\).
Chọn \(k = m - 1\) thì số đo cung \(AN = {255^0} + \left( {m - 1} \right){.360^0}\) \( = - {105^0} + m{360^0},m \in \mathbb{Z}\).
