Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {\dfrac{{{x^2} + 5x + 4}}{{2{x^2} + 3x + 1}}} \) là
-
A.
\({\rm{D}} = \left[ { - 4; - 1} \right) \cup \left( { - \dfrac{1}{2}; + \infty } \right).\)
-
B.
\({\rm{D}} = \left( { - \infty ; - 4} \right] \cup \left( { - 1; - \dfrac{1}{2}} \right).\)
-
C.
\({\rm{D}} = \left( { - \infty ; - 4} \right] \cup \left( { - \dfrac{1}{2}; + \infty } \right).\)
-
D.
\({\rm{D}} = \left[ { - 4; - \dfrac{1}{2}} \right).\)
Hàm số \(y = \sqrt {f\left( x \right)} \) xác định nếu \(f\left( x \right)\) xác định và \(f\left( x \right) \ge 0\).
Hàm số xác định khi và chỉ khi \(f\left( x \right) = \dfrac{{{x^2} + 5x + 4}}{{2{x^2} + 3x + 1}} \ge 0.\)
Phương trình \({x^2} + 5x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - \,4\end{array} \right.\) và \(2{x^2} + 3x + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \,1\\x = - \dfrac{1}{2}\end{array} \right..\)
Bảng xét dấu
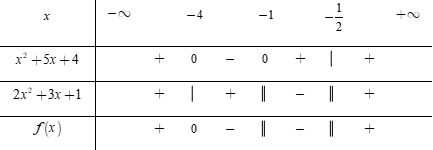
Dựa vào bảng xét dấu ta thấy \(\dfrac{{{x^2} + 5x + 4}}{{2{x^2} + 3x + 1}} \ge 0\)\( \Leftrightarrow x \in \left( { - \infty ; - 4} \right] \cup \left( { - \dfrac{1}{2}; + \infty } \right)\)
Vậy tập xác định của hàm số là \(D = \left( { - \infty ; - 4} \right] \cup \left( { - \dfrac{1}{2}; + \infty } \right).\)
Đáp án : C
